题目内容
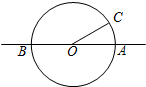 如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在圆O上,且∠AOC=30°,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q.如果QP=QO,则∠OCP的度数是
如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在圆O上,且∠AOC=30°,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q.如果QP=QO,则∠OCP的度数是考点:圆周角定理
专题:分类讨论
分析:分类讨论:如图1,设∠QOC=x,则∠QOP=x+30°,由QO=QP得到∠QPO=∠QOP=x+30°,再根据三角形外角性质得∠QCO=∠COP+∠CPO=x+60°,而OQ=OC,所以∠OQC=∠OCQ=x+60°,然后根据三角形内角和定理得x+x+60°+x+60°=180°,解得x=20°,再利用∠OCP=∠QOC+∠OQC进行计算即可;
利用同样的方法,解决如图2,如图3的情况.
利用同样的方法,解决如图2,如图3的情况.
解答:解:如图1,
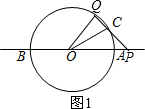
设∠QOC=x,则∠QOP=x+30°,
∵QO=QP,
∴∠QPO=∠QOP=x+30°,
∴∠QCO=∠COP+∠CPO=30°+x+30°=x+60°,
∵OQ=OC,
∴∠OQC=∠OCQ=x+60°,
∴x+x+60°+x+60°=180°,解得x=20°,
∴∠OCP=∠QOC+∠OQC=20°+20°+60°=100°;
如图2,
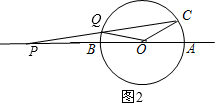
设∠QPO=x,
∵PQ=QO,
∴∠QOP=∠QPO=x,
∴∠CQO=2x,
而OC=OQ,
∴∠C=2x,
∵∠AOC=∠APC+∠C,
∴x+2x=30°,解得x=10°,
∴∠OCP=2x=20°;
如图3,
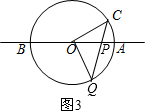
设∠QPO=x,
∵PQ=QO,
∴∠QOP=∠QPO=x,
∴∠Q=180°-2x,
∵OQ=OC,
∴∠C=180°-2x,
∵∠OPQ=∠C+∠POC,
∴180°-2x+30°=x,解得x=70°,
∴∠OCP=180°-2×70°=40°,
综上所述,∠OCP的度数为20°、40°或100°.
故答案为:20°、40°或100°.

设∠QOC=x,则∠QOP=x+30°,
∵QO=QP,
∴∠QPO=∠QOP=x+30°,
∴∠QCO=∠COP+∠CPO=30°+x+30°=x+60°,
∵OQ=OC,
∴∠OQC=∠OCQ=x+60°,
∴x+x+60°+x+60°=180°,解得x=20°,
∴∠OCP=∠QOC+∠OQC=20°+20°+60°=100°;
如图2,

设∠QPO=x,
∵PQ=QO,
∴∠QOP=∠QPO=x,
∴∠CQO=2x,
而OC=OQ,
∴∠C=2x,
∵∠AOC=∠APC+∠C,
∴x+2x=30°,解得x=10°,
∴∠OCP=2x=20°;
如图3,

设∠QPO=x,
∵PQ=QO,
∴∠QOP=∠QPO=x,
∴∠Q=180°-2x,
∵OQ=OC,
∴∠C=180°-2x,
∵∠OPQ=∠C+∠POC,
∴180°-2x+30°=x,解得x=70°,
∴∠OCP=180°-2×70°=40°,
综上所述,∠OCP的度数为20°、40°或100°.
故答案为:20°、40°或100°.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的性质.

练习册系列答案
相关题目
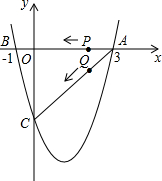 如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.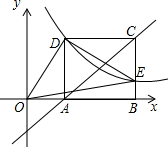 如图,已知正方形ABCD的边长为2,双曲线y=
如图,已知正方形ABCD的边长为2,双曲线y= 如图是随机抽查某校40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该校4000名同学一周参加体育锻炼时间达到9小时以上(含9小时)的人数是
如图是随机抽查某校40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该校4000名同学一周参加体育锻炼时间达到9小时以上(含9小时)的人数是 几个大小相同的小正方体搭成的一个几何体从正面看的形状如图所示,它的左视图是( )
几个大小相同的小正方体搭成的一个几何体从正面看的形状如图所示,它的左视图是( )


