题目内容
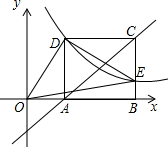 如图,已知正方形ABCD的边长为2,双曲线y=
如图,已知正方形ABCD的边长为2,双曲线y=| k |
| x |
考点:反比例函数综合题
专题:
分析:由正方形ABCD的边长为2,OD⊥DE,易证得△ADO≌△CDE(ASA),则可证得OA=CE,然后设点D(a,2),则点E(a+2,2-a),则可得2a=(a+2)(2-a),解此方程即可求得答案.
解答:解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=∠DAB=∠DCE=90°,
∴∠ADE+∠CDE=90°,
∵OD⊥DE,
∴∠ADO+∠ADE=90°,
∴∠ADO=∠CDE,
在△ADO和△CDE中,
,
∴△ADO≌△CDE(ASA),
∴OA=CE,
设点D(a,2),则点E(a+2,2-a),
∴2a=(a+2)(2-a),
解得:a=±
-1(负值舍去),
∴点D(
-1,2),
∴k=2a=2
-2.
故答案为:2
-2.
∴AD=CD,∠ADC=∠DAB=∠DCE=90°,
∴∠ADE+∠CDE=90°,
∵OD⊥DE,
∴∠ADO+∠ADE=90°,

∴∠ADO=∠CDE,
在△ADO和△CDE中,
|
∴△ADO≌△CDE(ASA),
∴OA=CE,
设点D(a,2),则点E(a+2,2-a),
∴2a=(a+2)(2-a),
解得:a=±
| 5 |
∴点D(
| 5 |
∴k=2a=2
| 5 |
故答案为:2
| 5 |
点评:此题属于反比例函数综合题,考查了待定系数法求函数的解析式、全等三角形的判定与性质以及正方形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
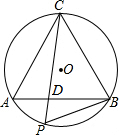 如图,等边△ABC内接于⊙O,点P是劣弧
如图,等边△ABC内接于⊙O,点P是劣弧
 如图,一艘科学考察船由港口A出发沿正北方向航行,在航线的一侧有两个小岛C、D.考察船在A处时,测得小岛C在船的正西方,小岛D在船的北偏西30°方向.考察船向北航行了12千米到B处时,测得小岛C在船的南偏西30°方向,小岛D在船的南偏西60°方向.求小岛C、D之间的距离.
如图,一艘科学考察船由港口A出发沿正北方向航行,在航线的一侧有两个小岛C、D.考察船在A处时,测得小岛C在船的正西方,小岛D在船的北偏西30°方向.考察船向北航行了12千米到B处时,测得小岛C在船的南偏西30°方向,小岛D在船的南偏西60°方向.求小岛C、D之间的距离. 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3)
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3)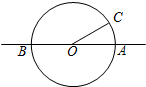 如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在圆O上,且∠AOC=30°,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q.如果QP=QO,则∠OCP的度数是
如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在圆O上,且∠AOC=30°,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q.如果QP=QO,则∠OCP的度数是 如图所示,数轴上在-2和-1之间的长度以小隔线分成八等分,A点在其中一隔,则A点表示的数是
如图所示,数轴上在-2和-1之间的长度以小隔线分成八等分,A点在其中一隔,则A点表示的数是