题目内容
已知等腰三角形的两边长分别为6和5，则它的周长等于 ．
考点：等腰三角形的性质,三角形三边关系
专题：
分析：分腰为6和腰为5两种情况，再求其周长．
解答：解：当腰为6时，则三角形的三边长分别为6、6、5，满足三角形的三边关系，周长为17；
当腰为5时，则三角形的三边长分别为5、5、6，满足三角形的三边关系，周长为16；
综上可知，等腰三角形的周长为16或17．
故答案为：16或17．
当腰为5时，则三角形的三边长分别为5、5、6，满足三角形的三边关系，周长为16；
综上可知，等腰三角形的周长为16或17．
故答案为：16或17．
点评：本题主要考查等腰三角形的性质，掌握等腰三角形的两腰相等是解题的关键．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
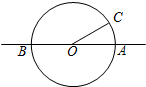如图，直线AB经过圆O的圆心，与圆O交于A、B两点，点C在圆O上，且∠AOC=30°，点P是直线AB上的一个动点（与点O不重合），直线PC与圆O相交于点Q．如果QP=QO，则∠OCP的度数是若单项式3a m+
b2与abn-1的和也是单项式，则点P（m+1，n-2）所在象限为（ ）
| 1 |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图，在△ABC中，∠C=2∠B，D是BC边上一点，且AD⊥AB．