题目内容
为了测量旗杆的高度AB，在离旗杆10米的C处，用高1.2米的测角仪CD测得旗杆顶部A的仰角为40°，求旗杆AB的高．（精确到0.1米）考点：解直角三角形的应用-仰角俯角问题
专题：
分析：由题可知，在直角三角形中，知道已知角和邻边，直接根据正切求出对边即可解决．
解答：解：∵CD⊥BC，AB⊥BC，DE⊥AB，
∴四边形DCBE是矩形，
∴DE=BC=10米，
在Rt△ADE中，
∵DE=10米，∠ADE=40°，
∴AE=DE•tan40°≈10×0.84=8.4（米），
∴AB=AE+BE=8.4+1.2=9.6（米）．
答：旗杆AB的高是9.6米．
∴四边形DCBE是矩形，
∴DE=BC=10米，
在Rt△ADE中，
∵DE=10米，∠ADE=40°，
∴AE=DE•tan40°≈10×0.84=8.4（米），
∴AB=AE+BE=8.4+1.2=9.6（米）．
答：旗杆AB的高是9.6米．
点评：本题考查的是解直角三角形的应用-仰角俯角问题，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
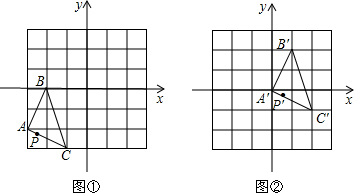
如图，把图①中的△ABC经过一定的变换得到图②中的△A′B′C′，如果图①中△ABC上点P的坐标为（a，b），那么这个点在图②中的对应点P′的坐标为（ ）
| A、（a+2，b+3） |
| B、（a-3，b-2） |
| C、（a+3，b+2） |
| D、（a-2，b-3） |
如图，点A，O，E在同一条直线上，∠AOB=40°，∠COD=28°，OD平分∠COE．
如图，在⊙O中，直径CD垂直于弦AB于E点，若AB=8，DE=2，求⊙O的半径．