题目内容
1.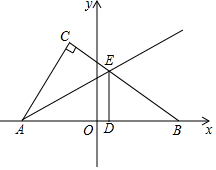 如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,∠ACB=90°,原点O是斜边AB的中点,直角边AC、BC的长分别是一元二次方程x2-14x+48=0的两个根(AC<BC),将Rt△ABC沿着AE折叠,使点C落在x轴上的点D处.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,∠ACB=90°,原点O是斜边AB的中点,直角边AC、BC的长分别是一元二次方程x2-14x+48=0的两个根(AC<BC),将Rt△ABC沿着AE折叠,使点C落在x轴上的点D处.(1)求点D的坐标.
(2)求折痕AE所在直线的解析式.
(3)若点P是射线AE上一个动点,在坐标平面内,是否存在一点M,使得以P、E、D、M为顶点,DE为底的直角梯形面积为8?若存在,请直接写出点M的坐标;若不存在,说明理由.
分析 (1)解方程可求得AC和BC的长,由勾股定理可求得AB的长,再结合折叠的性质可求得OD的长,则可求得D点坐标;
(2)可证明△BED∽△BAC,利用相似三角形的性质可求得DE,则可求得E点坐标,利用待定系数法可求得直线AE的解析式;
(3)可设M(x,0),则可表示出P点坐标,从而可表示出PM和DM的长,由梯形的面积可得到关于x的方程,可求得x的值,则可求得M点的坐标.
解答 解:
(1)解方程x2-14x+48=0,可得得x=6或x=8,
∵AC<BC,
∴AC=6,BC=8.
在Rt△ABC中,AB=10,
∵AD=AC=6,AO=$\frac{1}{2}$AB=5,
∴OD=AD-AO=1,
∴D(1,0);
(2)在Rt△BED中,∠EDB=90°,在Rt△ABC中,∠C=90°,
∴∠EBD=∠ABC,
∴△BED∽△BAC,
∴$\frac{BD}{BC}=\frac{ED}{AC}$.
∴ED=3,
∴E(1,3),
设直线AE的解析式为y=kx+b,
把A、E坐标代入可得$\left\{\begin{array}{l}-5k+b=0\\ k+b=3\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{1}{2}\\ b=\frac{5}{2}\end{array}\right.$,
∴直线AE的解析式为y=$\frac{1}{2}$x+$\frac{5}{2}$;
(3)存在.
∵四边形PEDM是以DE为底的直角梯形,
∴点M在x轴上,且PM⊥x轴,
设M(x,0)(x>-5),则P(x,$\frac{1}{2}$x+$\frac{5}{2}$),
∵点P在射线AE上,
∴PM=$\frac{1}{2}$x+$\frac{5}{2}$,DM=|x-1|,
∵E(1,3),
∴DE=3,
∵S梯形PEDM=8,
∴$\frac{1}{2}$(DE+PM)•DM=8,即$\frac{1}{2}$(3+$\frac{1}{2}$x+$\frac{5}{2}$)|x-1|=8,整理可得(11+x)|x-1|=32,
当点M在点D的左侧时,则(11+x)(1-x)=32,解得x=-7(舍去)或x=-3,此时M点坐标为(-3,0);
当点M在点D的右侧时,则(11+x)(x-1)=32,解得x=-5-2$\sqrt{17}$(舍去)或x=-5+2$\sqrt{17}$,此时M点的坐标为(-5+2$\sqrt{17}$);
综上可知存在满足条件的点M,其坐标为(-3,0)或($2\sqrt{17}-5,0$).
点评 本题为一次函数的综合应用,涉及一元二次方程的解法、直角三角形的性质、待定系数法、折叠的性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)中求得AD的长是解题的关键,在(2)中求得E点坐标是解题的关键,在(3)中用M的坐标表示出梯形的面积是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 53随堂测系列答案
53随堂测系列答案| A. | 2.41179×1011 | B. | 2.41179×1012 | C. | 2.41179×1013 | D. | 2.41179×1014 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 同角的余角相等 | B. | 同角的补角相等 | C. | 等角的余角相等 | D. | 等角的补角相等 |
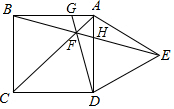 如图,在正方形ABCD的外侧作等边△ADE,连接BE交AC于点F,交AD于点H,连结DF并延长交AB于点G,下列结论中,正确的个数是( )
如图,在正方形ABCD的外侧作等边△ADE,连接BE交AC于点F,交AD于点H,连结DF并延长交AB于点G,下列结论中,正确的个数是( ) 如图,扇形的圆心角为120°,半径为6,将此扇形围成一个圆锥,则圆锥的底面半径为2.
如图,扇形的圆心角为120°,半径为6,将此扇形围成一个圆锥,则圆锥的底面半径为2.