题目内容
11. 如图,扇形的圆心角为120°,半径为6,将此扇形围成一个圆锥,则圆锥的底面半径为2.
如图,扇形的圆心角为120°,半径为6,将此扇形围成一个圆锥,则圆锥的底面半径为2.
分析 根据弧长公式求出扇形的弧长,根据圆锥的底面圆周长是扇形的弧长列式计算即可.
解答 解:设圆锥的底面半径为r,
扇形的弧长为:$\frac{120π×6}{180}$=4π,
则2πr=4π,
解得,r=2,
故答案为:2.
点评 本题考查的是圆锥的计算,掌握弧长公式、圆锥的底面圆周长是扇形的弧长是解题的关键.

练习册系列答案
相关题目
2.下列函数在每一个象限内y随x的增大而增大的是( )
| A. | y=-x+1 | B. | y=x2-1 | C. | y=$\frac{1}{x}$ | D. | y=2x |
3.在不透明的袋中有一些除颜色外完全相同的白色和黑色棋子,从中随机取出一颗棋子是白色棋子的概率是$\frac{1}{4}$;若从盒中取出3颗黑色棋子后,再随机取出一颗棋子是白色棋子的概率为$\frac{2}{5}$,则盒中白色棋子有( )
| A. | 1颗 | B. | 2颗 | C. | 3颗 | D. | 4颗 |
20.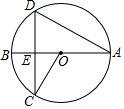 如图,AB是⊙0的直径,弦CD⊥AB于E,连结OC、AD,且∠A=35°,则∠AOC=( )
如图,AB是⊙0的直径,弦CD⊥AB于E,连结OC、AD,且∠A=35°,则∠AOC=( )
 如图,AB是⊙0的直径,弦CD⊥AB于E,连结OC、AD,且∠A=35°,则∠AOC=( )
如图,AB是⊙0的直径,弦CD⊥AB于E,连结OC、AD,且∠A=35°,则∠AOC=( )| A. | 70° | B. | 105° | C. | 110° | D. | 140° |
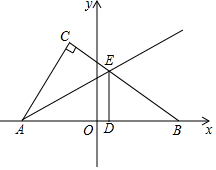 如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,∠ACB=90°,原点O是斜边AB的中点,直角边AC、BC的长分别是一元二次方程x2-14x+48=0的两个根(AC<BC),将Rt△ABC沿着AE折叠,使点C落在x轴上的点D处.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,∠ACB=90°,原点O是斜边AB的中点,直角边AC、BC的长分别是一元二次方程x2-14x+48=0的两个根(AC<BC),将Rt△ABC沿着AE折叠,使点C落在x轴上的点D处. 如图,在正方形ABCD中,F是CD的中点,连接BF,将△BCF沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则sin∠BQP的值为$\frac{4}{5}$.
如图,在正方形ABCD中,F是CD的中点,连接BF,将△BCF沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则sin∠BQP的值为$\frac{4}{5}$. 如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中: