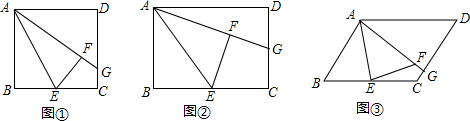
题目内容
操作:如图①在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD内部,延长AF交CD于点G.易知FG=GC.
探究:若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段GF与GC相等吗?请说明理由.
拓展:如图③,将图①中的正方形ABCD改为平行四边形,其他条件不变,若AB=3,AD=4,则△AGD的周长为 .
探究:若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段GF与GC相等吗?请说明理由.
拓展:如图③,将图①中的正方形ABCD改为平行四边形,其他条件不变,若AB=3,AD=4,则△AGD的周长为

考点:四边形综合题
专题:
分析:求出EF=BE=CE,推出∠EFC=∠ECF,推出∠EFG=∠ECG,相减即可;求出EF=BE=CE,推出∠EFC=∠ECF,推出∠EFG=∠ECG,相减,求出FG=CG,即可得出三角形AGD的周长等于AD+DC+AF,代入求出即可.
解答:解:探究:GF=GC,
理由是:连接CF,
∵四边形ABCD是矩形,
∴∠B=∠ECG=90°,
∵△ABE沿AE折叠后得到△AFE,
∴∠B=∠AFE,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠AFE+∠GFE=180°,
∴∠C=∠GFE,
∵∠EFC=∠ECF,
∴∠GFC=∠GCF,
∴GF=GC.
拓展:∵四边形ABCD是平行四边形,
∴AB=CD=3=AF,
∵AD=4,
∴△AGD的周长是AD+DG+AF=4+DG+AF+FG=4+DG+CG+AF=4+3+3=10.
故答案为:10.
理由是:连接CF,
∵四边形ABCD是矩形,
∴∠B=∠ECG=90°,
∵△ABE沿AE折叠后得到△AFE,
∴∠B=∠AFE,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠AFE+∠GFE=180°,
∴∠C=∠GFE,
∵∠EFC=∠ECF,
∴∠GFC=∠GCF,
∴GF=GC.
拓展:∵四边形ABCD是平行四边形,
∴AB=CD=3=AF,
∵AD=4,
∴△AGD的周长是AD+DG+AF=4+DG+AF+FG=4+DG+CG+AF=4+3+3=10.
故答案为:10.
点评:本题考查了矩形性质,平行四边形的性质,等于三角形的性质和判定等知识点的应用,主要考查学生的推理和计算能力,题目比较好,综合性比较强.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
一个不透明的袋子里有4个颜色不同的球,其中2个红球,1个白球,1个黑球,搅匀后从袋里摸出两个球,摸到的两个球恰为一红一黑的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在-2.5,3,-1.5,0这四个数中,最小的数是( )
| A、-2.5 | B、3 |
| C、-1.5 | D、0 |
 如图,已知点A的坐标为(
如图,已知点A的坐标为(| 3 |
| k |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
 如图,在直角梯形ABCD中,AB⊥BC,AE∥DC交BC于点E,O是AC的中点,连接BO交AE于点H,AB=
如图,在直角梯形ABCD中,AB⊥BC,AE∥DC交BC于点E,O是AC的中点,连接BO交AE于点H,AB=