题目内容
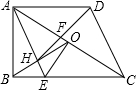 如图,在直角梯形ABCD中,AB⊥BC,AE∥DC交BC于点E,O是AC的中点,连接BO交AE于点H,AB=
如图,在直角梯形ABCD中,AB⊥BC,AE∥DC交BC于点E,O是AC的中点,连接BO交AE于点H,AB=| 3 |
| 1 |
| 2 |
| HF |
| DF |
| 3 |
| 4 |
| A、①②③④ | B、①③④ |
| C、①② | D、①②③ |
考点:四边形综合题
专题:压轴题
分析:①根据条件四边形ABCD是直角梯形就可以得出AD∥BC,有AE∥CD就可以得出四边形AECD是平行四边形,由勾股定理可以求出AE=AD=2,就可以求出四边形AECD是菱形;
②由条件可以求出S四ABED=S△ABE+
S△AEC=
+
=
,S四ABCD=
(2+3)
=
,
S四ABCD=
≠
而得出结论;
③由AB=
,BC=3就有tan∠ACB=
,得出∠ACB=30°.就有∠BAC=60°,由O是AC的中点就可以得出△ABO是等边三角形,就有∠ABO=60°,由三角函数值可以得出∠AEB=60°,可以求出∠BHE=90°,从而得出BO⊥AE,从而得出BO⊥CD;
④作HG⊥AC于G,通过勾股定理可以求出AE、EH的值,就可以得出HG的值,根据菱形的性质可以得出OD的值,再由三角形相似就可以得出结论.
②由条件可以求出S四ABED=S△ABE+
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
5
| ||
| 2 |
| 1 |
| 2 |
5
| ||
| 4 |
| 3 |
③由AB=
| 3 |
| ||
| 3 |
④作HG⊥AC于G,通过勾股定理可以求出AE、EH的值,就可以得出HG的值,根据菱形的性质可以得出OD的值,再由三角形相似就可以得出结论.
解答:解:①∵四边形ABCD是直角梯形,
∴AD∥BC.
∵AE∥DC,
∴四边形AECD是平行四边形,
∴AD=CE.
∵AD=2,BC=3,
∴CE=2,BE=1.
∵AB⊥BC,
∴∠ABC=90°.
在Rt△ABE中,由勾股定理,得
AE=
=2.
∴AD=AE,
∴四边形AECD是菱形;
②∵四边形AECD是菱形,O是AC的中点,
∴EO⊥AC,AO=OC,∠ACE=∠EAC=∠CAD=∠ACD.
∵AB=
,BC=3,
∴tan∠ACB=
,
∴∠ACB=30°,
∴∠ACE=∠EAC=∠CAD=∠ACD=30°
∴∠BAC=60°,EO=
AE=1,
∴由勾股定理,得AO=
.
∴S四边形ABEO=S△ABE+S△AOE=
+
=
.
∵S梯形ABCD=
(2+3)
=
,
∴
S梯形ABCD=
≠
,故②错误;
③∵AO=AB=
,且∠BAC=60°,
∴△ABO为等边三角形,
∴∠ABO=60°,∠BAE=30°,
∴∠AHB=90°,
∴BO⊥AE,
∵AE∥CD,
∴BO⊥CD,故③正确;
∴BH=
,
∴AH=
.
④作HG⊥AC于G,连结OD,
∴∠AGH=∠OGH=∠AOG=90°,
在Rt△AGH中,∠EAC=30°,
∴HG=
.
∵O是中点,AD=CD,
∴DO⊥AC,
∴∠AOD=90°,OD=
DC=1.
∴∠HGF=∠DOF=90°,
∵∠GFH=∠DFO,
∴△GFH∽△OFD,
∴
=
,
∴
=
,
∴
=
,故④正确
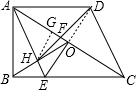
综上所述,正确的有①③④.
故选B.
∴AD∥BC.
∵AE∥DC,
∴四边形AECD是平行四边形,
∴AD=CE.
∵AD=2,BC=3,
∴CE=2,BE=1.
∵AB⊥BC,
∴∠ABC=90°.
在Rt△ABE中,由勾股定理,得
AE=
| 3+1 |
∴AD=AE,
∴四边形AECD是菱形;
②∵四边形AECD是菱形,O是AC的中点,
∴EO⊥AC,AO=OC,∠ACE=∠EAC=∠CAD=∠ACD.
∵AB=
| 3 |
∴tan∠ACB=
| ||
| 3 |
∴∠ACB=30°,
∴∠ACE=∠EAC=∠CAD=∠ACD=30°
∴∠BAC=60°,EO=
| 1 |
| 2 |
∴由勾股定理,得AO=
| 3 |
∴S四边形ABEO=S△ABE+S△AOE=
| ||
| 2 |
| ||
| 2 |
| 3 |
∵S梯形ABCD=
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
∴
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
| 3 |
③∵AO=AB=
| 3 |
∴△ABO为等边三角形,
∴∠ABO=60°,∠BAE=30°,
∴∠AHB=90°,
∴BO⊥AE,
∵AE∥CD,
∴BO⊥CD,故③正确;
∴BH=
| ||
| 2 |
∴AH=
| 3 |
| 2 |
④作HG⊥AC于G,连结OD,
∴∠AGH=∠OGH=∠AOG=90°,
在Rt△AGH中,∠EAC=30°,
∴HG=
| 3 |
| 4 |
∵O是中点,AD=CD,
∴DO⊥AC,
∴∠AOD=90°,OD=
| 1 |
| 2 |
∴∠HGF=∠DOF=90°,
∵∠GFH=∠DFO,
∴△GFH∽△OFD,
∴
| GH |
| OD |
| HF |
| DF |
∴
| ||
| 1 |
| HF |
| DF |
∴
| HF |
| DF |
| 3 |
| 4 |

综上所述,正确的有①③④.
故选B.
点评:本题是一道四边形的综合试题,考查了梯形的性质的运用,直角三角形的性质的运用,勾股定理的运用,等边三角形的判定及性质的运用,相似三角形的判定及性质的运用.解答本题合理利用30°的直角三角形的性质和作辅助线是关键.

练习册系列答案
相关题目
下列四个图形中是三棱柱的表面展开图的是( )
A、 |
B、 |
C、 |
D、 |
下列计算正确的是( )
| A、a2+a2=2a2 |
| B、a3•a2=a6 |
| C、a6÷a3=a2 |
| D、(3a)3=9a3 |
 已知:如图,点A,B在直线CD上,AE∥BF,∠CAE=110°,则∠DBF的度数为( )
已知:如图,点A,B在直线CD上,AE∥BF,∠CAE=110°,则∠DBF的度数为( )| A、50° | B、55° |
| C、60° | D、70° |
 如图,直线y=k1x+b与双曲线
如图,直线y=k1x+b与双曲线
 如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.
如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.