题目内容
15. 如图,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是π-1.
如图,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是π-1.
分析 已知BC为直径,则∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D为半圆的中点,阴影部分的面积可以看做是扇形ACB的面积与△ADC的面积之差.
解答 解:在Rt△ACB中,AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵BC是半圆的直径,
∴∠CDB=90°,
在等腰Rt△ACB中,CD垂直平分AB,CD=BD=$\sqrt{2}$,
∴D为半圆的中点,
S阴影部分=S扇形ACB-S△ADC=$\frac{1}{4}$π×22-$\frac{1}{2}$×($\sqrt{2}$)2=π-1.
故答案为π-1.
点评 本题考查扇形面积的计算公式及不规则图形面积的求法,掌握面积公式是解题的关键.

练习册系列答案
相关题目
10.中华人民共和国的陆地面积为9600000km2,9600000这个数用科学记数法表示为( )
| A. | 9.6×105 | B. | 96×105 | C. | 9.6×106 | D. | 96×106 |
4.无锡某校准备组织学生及学生家长到上海进行社会实践,为了便于管理,所有人员必须乘坐在同一列高铁上;根据报名人数,若都买一等座单程火车票需6175元,若都买二等座单程火车票且花钱最少,则需3150元;已知学生家长与教师的人数之比为2:1,无锡到上海的火车票价格(高铁学生票只有二等座可以打7.5折)如表所示:
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买一个单程火车票至少要花多少钱?最多要花多少钱?
| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 |
| 无锡 | 上海 | 95(元) | 60(元) |
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买一个单程火车票至少要花多少钱?最多要花多少钱?
5.已知a、b是一元次方程x2-2x-3=0的两个根,则a2b+ab2的值是( )
| A. | -1 | B. | -5 | C. | -6 | D. | 6 |
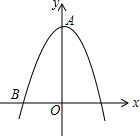 如图,抛物线y=ax2+c经过点A(0,2)和点B(-1,0).
如图,抛物线y=ax2+c经过点A(0,2)和点B(-1,0).