题目内容
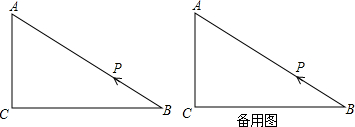
5.已知:如图,∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B.
(1)在图1中,过点C作CE⊥CB,与直线MN于点E,
①依题意补全图形;
②求证:△BCE是等腰直角三角形;
③图1中,线段BD、AB、CB满足的数量关系是BD+AB=$\sqrt{2}$CB;
(2)当MN绕A旋转到如图(2)和图(3)两个位置时,其它条件不变.
在图2中,线段BD、AB、CB满足的数量关系是AB-BD=$\sqrt{2}$CB;
在图3中,线段BD、AB、CB满足的数量关系是BD-AB=$\sqrt{2}$CB;
(3)MN在绕点A旋转过程中,当∠BCD=30°,BD=$\sqrt{2}$时,则CB=$\sqrt{3}$-1或$\sqrt{3}$+1.
分析 (1)①依题意补全图形如图所示,②判断出△CAE≌△CDB,即得结论,③过点C作CE⊥CB,得到∠BCD=∠ACE,判断出△ACE≌△DCB,确定△ECB为等腰直角三角形即可.
(2)①过点C作CE⊥CB于点C,判断出△ACE≌△DCB,确定△ECB为等腰直角三角形;②解题思路同(1)③,过点C作CE⊥CB于点C,得到△ACE≌△DCB,从而确定△ECB为等腰直角三角形;
(3)由(1)③,得△ACE≌△BCD,CE=BC,得到△BCE为等腰直角三角形,得到BD=$\sqrt{2}$BH=$\sqrt{2}$,求出BH,再用勾股定理即可.
解答 解:(1)①依题意补全图形如下图,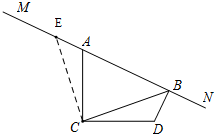
②证明:
∵∠ACD=90°,
又∵CE⊥CB,
∴∠ECB=90°=∠ACD,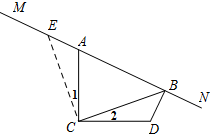
∴∠1=∠2.
∵DB⊥MN于点B,
∴∠ABD=90°,
∴∠BAC+∠D=180°.
又∵∠BAC+∠EAC=180°,
∴∠D=∠EAC.
∴△CAE≌△CDB,
∴CE=CB.
③如图(1),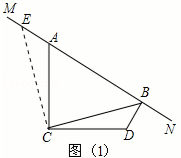
过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵DB⊥MN
∴∠ABC+∠CBD=90°,
∵CE⊥CB
∴∠ABC+∠CEA=90°,
∴∠CBD=∠CEA.
又∵AC=DC,
∴△ACE≌△DCB(AAS),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=$\sqrt{2}$CB.
又∵BE=AE+AB,
∴BE=BD+AB,
∴BD+AB=$\sqrt{2}$CB,
故答案为BD+AB=$\sqrt{2}$CB
(2)①如图(2),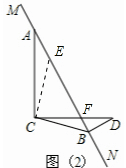
过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,∠ECB=90°,
∴∠ACE=90°-∠DCE,∠BCD=90°-∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,
$\left\{\begin{array}{l}{∠BCD=∠ACE}\\{AC=DC}\\{∠CAE=∠D}\end{array}\right.$,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=$\sqrt{2}$CB.
又∵BE=AB-AE,
∴BE=AB-BD,
∴AB-BD=$\sqrt{2}$CB.
②BD-AB=$\sqrt{2}$CB.
如图(3),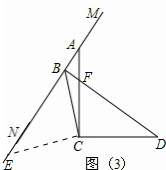
过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,∠BCE=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,
$\left\{\begin{array}{l}{∠BCD=∠ACE}\\{AC=DC}\\{∠CAE=∠D}\end{array}\right.$
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=$\sqrt{2}$CB.
又∵BE=AE-AB,
∴BE=BD-AB,
∴BD-AB=$\sqrt{2}$CB.
故答案为AB-BD=$\sqrt{2}$CB和BD-AB=$\sqrt{2}$CB.
(3)①如图4,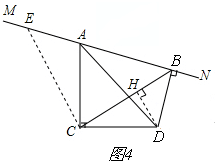
由(1)③,得△ACE≌△BCD,CE=BC,
∴△BCE为等腰直角三角形,
∴∠AEC=45°=∠CBE=∠DBC,
过点D作DH⊥BC,
∴△DHB是等腰直角三角形,
∴BD=$\sqrt{2}$BH=$\sqrt{2}$,
∴BH=DH=1,
在Rt△CDH中,∠BCD=30°,BH=1,
∴CH=$\sqrt{3}$,
∴BC=CH+BH=$\sqrt{3}$+1;
②如图5,过点D作DH⊥BC交CB的延长线与H,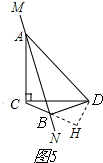
同①的方法,得,CH=$\sqrt{3}$,BH=1,
∴BC=CH-BH=$\sqrt{3}$-1.
故答案为$\sqrt{3}-1$或$\sqrt{3}+1$.
点评 本题是几何变换综合题,主要考查了三角形全等的判定和性质,等腰直角三角形的判定和性质等.解本题的关键是作出辅助线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 监测点 | 荔园 | 西乡 | 华侨城 | 南油 | 盐田 | 龙岗 | 洪湖 | 南澳 | 葵涌 | 梅沙 | 观澜 |
| AQI | 15 | 31 | 25 | 24 | 31 | 24 | 25 | 25 | 34 | 20 | 26 |
| 质量 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 |
| A. | 25,25 | B. | 31,25 | C. | 25,24 | D. | 31,24 |
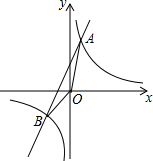 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).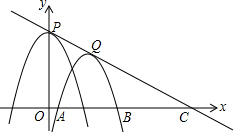 如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.
如图,点P是抛物线y=-x2+4的顶点,将抛物线平移,平移后的抛物线与x轴交于A,B两点(A在B的左侧)顶点Q落在第一象限内,且△ABQ是等边三角形,直线PQ与x轴交于点C,若PQ=$\sqrt{3}$,则BC=3$\sqrt{2}$-$\sqrt{3}$.