题目内容
19．分解因式：1-b-a2+a3b+a2b3-a3b3=（1-b）（1-a2-a2b-a2b2+a3b+a2b2）．分析 将已知代数式分为3组：（1-b）、（-a2+a2b3）、（a3b-a3b3），利用提取公因式法进行因式分解．
解答 解：原式=（1-b）-（a2-a2b3）+（a3b-a3b3），
=（1-b）-a2（1-b3）+a3b（1-b2），
=（1-b）-a2（1-b）（1+b+b2）+a3b（1+b）（1-b），
=（1-b）[1-a2（1+b+b2）+a3b（1-b）]，
=（1-b）（1-a2-a2b-a2b2+a3b+a2b2）．
故答案是：（1-b）（1-a2-a2b-a2b2+a3b+a2b2）．
点评 本题考查了分组分解法分解因式，分组分解法一般是针对四项或四项以上多项式的因式分解，分组有两个目的，一是分组后能出现公因式，二是分组后能应用公式．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
抛物线y=x2-mx-3与x轴交于点A、B，与y轴交于点C，其中点A的坐标为（1+m，0）．
如图，已知DE为△ABC中位线，点F在DE上，且∠AFB=90°，AB=4，BC=6，则EF长为1．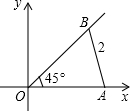
在平面直角坐标系xOy中，点A是x轴正半轴上任意一点，点B是第一象限角平分线上一点（不含原点），AB=2，∠AOB=45°，以AB为一边作正△ABC，则