题目内容
10.计算(1)1022(用简便方法)
(2)a3•a3+(2a3)2+(-a2)3
(3)|-3|+(-1)2013×(π-3)0-($\frac{1}{2}$)-1
(4)先化简,再求值:已知3x2-x-4=0,求(x-1)(2x-1)+(x+1)2+1的值.
分析 (1)先变形,再根据完全平方公式进行计算即可;
(2)先算乘方,再算乘法,最后合并同类项即可;
(3)先算乘方,再算加减即可;
(4)先算乘法,再合并同类项,最后代入求出即可.
解答 解:(1)1022
=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10404;
(2)a3•a3+(2a3)2+(-a2)3
=a6+4a6-a6
=4a6;
(3)|-3|+(-1)2013×(π-3)0-($\frac{1}{2}$)-1
=3-1×1-2
=0;
(4)(x-1)(2x-1)+(x+1)2+1
=2x2-x-2x+1+x2+2x+1+1
=3x2-x+3,
∵3x2-x-4=0,
∴3x2-x=4,
∴原式=4+3=7.
点评 本题考查了完全平方公式,零指数幂,负整数指数幂,绝对值,整式的混合运算和求值的应用,能灵活运用知识点进行计算和化简是解此题的关键,注意运算顺序.

练习册系列答案
相关题目
15.下列等式中,从左到右的变形是分解因式的是( )
| A. | (x+1)(x-2)=x2-x-2 | B. | 4a2b3=4a2•b3 | C. | x2-2x+1=(x-1)2 | D. | x2-3x+2=x(x-3)+2 |
 如图,已知线段a,b和∠α,求作一个三角形,使其有一个内角等于α,且∠α的对边等于a,另一边等于b,要保留作图痕迹,写出作法.
如图,已知线段a,b和∠α,求作一个三角形,使其有一个内角等于α,且∠α的对边等于a,另一边等于b,要保留作图痕迹,写出作法.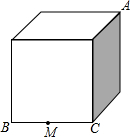 如图正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为$\sqrt{13}$.
如图正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为$\sqrt{13}$.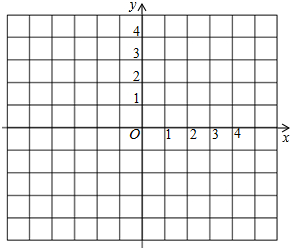 如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).