题目内容
6.已知二次函数y=-2x2+bx+c图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
分析 (1)由题意可知抛物线的解析式为y=-2(x-3)2+8,由此求出b、c即可解决问题.
(2)设M(m,n),由题意$\frac{1}{2}$•3•|n|=9,可得n=±6,分两种情形列出方程求出m的值即可;
解答 解:(1)由题意抛物线的顶点坐标(3,8),
∴抛物线的解析式为y=-2(x-3)2+8=-2x2+12x-10,
∴b=12,c=-10,
∴b+2c+8=12-20+8=0,
∴不等式b+2c+8≥0成立.
(2)设M(m,n),
由题意$\frac{1}{2}$•3•|n|=9,
∴n=±6,
①当n=6时,6=-2m2+12m-10,
解得m=2或4,
②当n=-6时,-6=-2m2+12m-10,
解得m=3±$\sqrt{7}$,
∴满足条件的点M的坐标为(2,6)或(4,6)或(3+$\sqrt{7}$,-6)或(3-$\sqrt{7}$,-6).
点评 本题考查抛物线与x轴的交点、二次函数图象与系数的关系等知识,解题的关键是熟练掌握二次函数的三种形式,学会利用参数构建方程解决问题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
18.一组数据5,7,8,10,12,12,44的众数是( )
| A. | 10 | B. | 12 | C. | 14 | D. | 44 |
15.如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
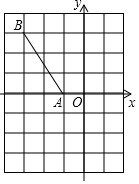 如图,线段AB的两个顶点都在方格纸的格点上,建立直角坐标系后点A的坐标是(-1,0),将线段AB绕点A顺时针旋转180°,则旋转后点B的对应点的坐标是(1,-3).
如图,线段AB的两个顶点都在方格纸的格点上,建立直角坐标系后点A的坐标是(-1,0),将线段AB绕点A顺时针旋转180°,则旋转后点B的对应点的坐标是(1,-3).