题目内容
7.已知△ABC为直角三角形,且AB=AC=$\sqrt{2}$,则这个三角形斜边上的高为1.分析 先根据勾股定理求得斜边长,再根据面积法即可得到这个三角形斜边上的高.
解答 解:∵△ABC为直角三角形,且AB=AC=$\sqrt{2}$,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=2,
设这个三角形斜边上的高为h,则
$\frac{1}{2}$AB×AC=$\frac{1}{2}$BC×h,
∴h=$\frac{AB×AC}{BC}$=$\frac{\sqrt{2}×\sqrt{2}}{2}$=1,
故答案为:1.
点评 本题主要考查了等腰直角三角形的性质的运用,解决问题的关键是面积法的灵活运用.

练习册系列答案
相关题目
12.下列调查中,最适合采用普查方式的是( )
| A. | 对太湖流域水质情况的调查 | |
| B. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C. | 对一个城市每天丢弃塑料袋数量的调查 | |
| D. | 对无锡电视台某栏目收视率的调查 |
16.下列说法正确的是( )
| A. | 从一个不透明的袋子里面挑球,连续10次都摸出红球,那么袋子里面只有红球 | |
| B. | 天气预报“明天降水概率25%”,是指明天有25%的时间会下雨 | |
| C. | 某种福利彩票,中奖率是千分之一,买这种彩票1000张,一定会中奖 | |
| D. | 连续投一枚硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 |
 如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为1.
如图,在矩形ABCD中,AB=5,AD=3.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB'C'D'.若点B的对应点B'落在边CD上,则B'C的长为1. 如图,已知正比例函数与反比例函数的图象在第一象限的交点为A(2,4).
如图,已知正比例函数与反比例函数的图象在第一象限的交点为A(2,4). 如图,半圆的圆心为O,直径AB的长为12,C为半圆上一点,∠CAB=30°,$\widehat{AC}$的长是4π.
如图,半圆的圆心为O,直径AB的长为12,C为半圆上一点,∠CAB=30°,$\widehat{AC}$的长是4π.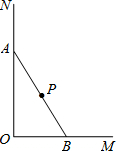 如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )
如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )