题目内容
11.(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论.

分析 (1)根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AMB的度数,根据直角三角形锐角的关系,可得∠ABM与∠BAM的关系,根据同角的余角相等,可得∠BAM与∠CBF的关系,根据ASA,可得△ABE≌△BCF,根据全等三角形的性质,可得答案;
(2)根据矩形的性质得到∠ABC=∠C,由余角的性质得到∠BAM=∠CBF,根据相似三角形的性质即可得到结论.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠C,AB=BC.
∵AE⊥BF,
∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,
∴∠BAM=∠CBF.
在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠BAE=∠CBF}\\{AB=CB}\\{∠ABE=∠BCF}\end{array}\right.$,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)解:AE=$\frac{2}{3}$BF,
理由:∵四边形ABCD是矩形,
∴∠ABC=∠C,
∵AE⊥BF,
∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,
∴∠BAM=∠CBF,
∴△ABE∽△BCF,
∴$\frac{AE}{BF}=\frac{AB}{BC}$=$\frac{2}{3}$,
∴AE=$\frac{2}{3}$BF.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
1. 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )| A. | 14cm | B. | 11cm | C. | 6cm | D. | 3cm |
16.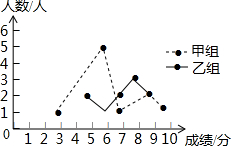 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
(1)求出下列成绩统计分析表中a,b的值:
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.(1)求出下列成绩统计分析表中a,b的值:
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.8 | a | 3.76 | 90% | 30% |
| 乙组 | b | 7.5 | 1.96 | 80% | 20% |
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
3.已知下列命题:
①若$\frac{a}{b}$>1,则a>b;
②若a+b=0,则|a|=|b|;
③等边三角形的三个内角都相等;
④底角相等的两个等腰三角形全等.
其中原命题与逆命题均为真命题的个数是( )
①若$\frac{a}{b}$>1,则a>b;
②若a+b=0,则|a|=|b|;
③等边三角形的三个内角都相等;
④底角相等的两个等腰三角形全等.
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列调查中,最适合采用普查方式的是( )
| A. | 对太湖流域水质情况的调查 | |
| B. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C. | 对一个城市每天丢弃塑料袋数量的调查 | |
| D. | 对无锡电视台某栏目收视率的调查 |
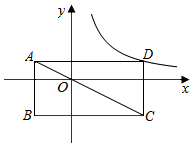 如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上.若点B的坐标为(-2,-2),则k=4.
如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上.若点B的坐标为(-2,-2),则k=4.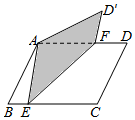 如图,?ABCD中,∠B=60°,AB=3,BC=4,折叠?ABCD使C落在A处,折痕为EF,点E、F分别在BC、AD上,则AF=$\frac{13}{5}$.
如图,?ABCD中,∠B=60°,AB=3,BC=4,折叠?ABCD使C落在A处,折痕为EF,点E、F分别在BC、AD上,则AF=$\frac{13}{5}$.