题目内容
18.对于任意实数a,b,定义关于“?”的一种运算如下:a?b=2a-b.例如:5?2=2×5-2=8,(-3)?4=2×(-3)-4=-10.(1)若3?x=-2011,求x的值;
(2)若x?3<5,求x的取值范围.
分析 (1)根据新定义列出关于x的方程,解之可得;
(2)根据新定义列出关于x的一元一次不等式,解之可得.
解答 解:(1)根据题意,得:2×3-x=-2011,
解得:x=2017;
(2)根据题意,得:2x-3<5,
解得:x<4.
点评 本题主要考查解一元一次方程和一元一次不等式不等式的能力,根据题意列出方程和不等式是解题的关键.

练习册系列答案
相关题目
13.一元一次不等式组$\left\{\begin{array}{l}2x>x-1\\ \frac{1}{2}x≤1\end{array}\right.$的解集是( )
| A. | x>-1 | B. | x≤2 | C. | -1<x≤2 | D. | x>-1或x≤2 |
3.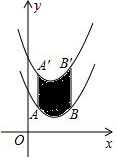 如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
 如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )| A. | $y=\frac{1}{2}{({x-2})^2}-2$ | B. | $y=\frac{1}{2}{({x-2})^2}+7$ | C. | $y=\frac{1}{2}{({x-2})^2}-5$ | D. | $y=\frac{1}{2}{({x-2})^2}+4$ |
7.函数y=$\frac{x}{2-x}$中自变量x的取值范围是( )
| A. | x≠2 | B. | x≥2 | C. | x≤2 | D. | x>2 |
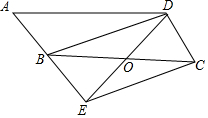 如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.