题目内容
3.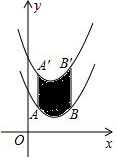 如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
如图,将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )| A. | $y=\frac{1}{2}{({x-2})^2}-2$ | B. | $y=\frac{1}{2}{({x-2})^2}+7$ | C. | $y=\frac{1}{2}{({x-2})^2}-5$ | D. | $y=\frac{1}{2}{({x-2})^2}+4$ |
分析 先根据二次函数图象上点的坐标特征求出A、B两点的坐标,再过A作AC∥x轴,交B′B的延长线于点C,则C(4,1$\frac{1}{2}$),AC=4-1=3,根据平移的性质以及曲线段AB扫过的面积为9(图中的阴影部分),得出AA′=3,然后根据平移规律即可求解.
解答 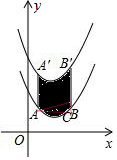
解:∵函数y=$\frac{1}{2}$(x-2)2+1的图象过点A(1,m),B(4,n),
∴m=$\frac{1}{2}$(1-2)2+1=1$\frac{1}{2}$,n=$\frac{1}{2}$(4-2)2+1=3,
∴A(1,1$\frac{1}{2}$),B(4,3),
过A作AC∥x轴,交B′B的延长线于点C,则C(4,1$\frac{1}{2}$),
∴AC=4-1=3,
∵曲线段AB扫过的面积为9(图中的阴影部分),
∴AC•AA′=3AA′=9,
∴AA′=3,
即将函数y=$\frac{1}{2}$(x-2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,
∴新图象的函数表达式是y=$\frac{1}{2}$(x-2)2+4.
故选D.
点评 此题主要考查了二次函数图象与几何变换以及平行四边形面积求法等知识,根据已知得出AA′是解题关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
13.“六一”期间,某文具店欲购进A、B两种型号的文具共100只进行销售,其进价和售价之间的关系如表:若该文具店购进A种型号的文具x只,销售完这批文具后所获得的利润为y元.
(1)求y与x的函数关系式;
(2)由于资金紧缺,在实际进货时进货款不得超过1380元,则该文具店销售完这批文具后所能获得最大利润为多少?
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 12 | 18 |
| B型 | 15 | 23 |
(2)由于资金紧缺,在实际进货时进货款不得超过1380元,则该文具店销售完这批文具后所能获得最大利润为多少?
11.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
| A. | 0<y1<y2 | B. | y1<0<y2 | C. | y1<y2<0 | D. | y2<0<y1 |
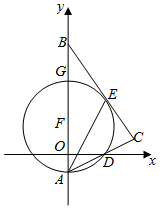 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G. 如图是我市某连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是11℃.
如图是我市某连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是11℃.