题目内容
20.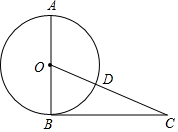 如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,
如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,(1)求⊙O的半径;
(2)连接AD并延长,交BC于点E,取BE的中点F,连接DF,试判断DF与⊙O的位置关系,并说明理由.
分析 (1)设⊙O的半径为R,由切线的性质得出∠OBC=90°,由勾股定理得出方程,解方程即可;
(2)连接BD,由等腰三角形的性质得出∠OBD=∠ODB,由圆周角定理得出∠ADB=90°,求出∠BDE=90°,由直角三角形的性质得出DF=$\frac{1}{2}$BE=BF,得出∠DBF=∠BDF,证出∠BDF+∠ODB=90°,即可得出结论.
解答 解:(1)设⊙O的半径为R,
∵BC是⊙O的切线,
∴∠OBC=90°,
∴OB2+BC2=OC2,
即R2+42=(R+2)2,
解得:R=3,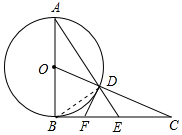
即⊙O的半径为3;
(2)DF与⊙O相切;理由如下:
如图所示:连接BD,
∵OB=OD,
∴∠OBD=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BDE=90°,
∵F是BE的中点,
∴DF=$\frac{1}{2}$BE=BF,
∴∠DBF=∠BDF,
∵∠DBF+∠OBD=90°,
∴∠BDF+∠ODB=90°,
∴DF⊥OD,
∴DF与⊙O相切.
点评 本题考查了切线的性质与判定、勾股定理、等腰三角形的性质、直角三角形的性质等知识;熟练掌握切线的判定与性质是解决问题的突破口.

练习册系列答案
相关题目
5.调查显示,截止2015年底某市汽车拥有量为16.9万辆,已知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
| A. | 10(1+x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1-x)2=16.9 | D. | 10(1-2x)=16.9 |
12.在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50,如果乙得到甲所有钱的$\frac{2}{3}$,那么乙也共有钱50.甲、乙两人各需带多少钱?设甲需带钱x,乙带钱y,根据题意可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{1}{2}x+y=50}\\{x+\frac{2}{3}y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+\frac{1}{2}y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ |
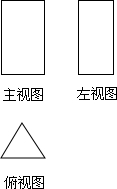 (1)如图所示为一几何体的三视图:
(1)如图所示为一几何体的三视图: 如图,某英语单词由四个字母组成,且四个字母都关于直线l对称,则这个英语单词的汉语意思为书.
如图,某英语单词由四个字母组成,且四个字母都关于直线l对称,则这个英语单词的汉语意思为书.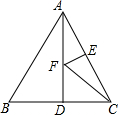 如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.
如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-2(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴负半轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-2(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴负半轴交于点D.