题目内容
11.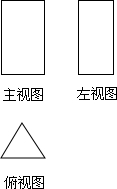 (1)如图所示为一几何体的三视图:
(1)如图所示为一几何体的三视图:①写出这个几何体的名称;
②画出这个几何体的一种表面展开图;
③若长方形的高为10cm,正三角形的边长为4cm,求这个几何体的侧面积.
(2)方程$\frac{3}{2}$[(a-$\frac{5}{3}$)x+$\frac{1}{2}$]=1和方程$\frac{1.7-2x}{0.3}$-1=$\frac{0.8+x}{0.6}$的解相同,求a的值.
分析 (1)①如图所示,根据三视图的知识来解答;②根据几何体画出这个几何体的一种表面展开图即可;③根据求图形的面积的方法即可得到结果;
(2)根据题意即可得到结论.
解答  解:(1)①根据俯视图为三角形,主视图以及左视图都是矩形,可得这个几何体为三棱柱;
解:(1)①根据俯视图为三角形,主视图以及左视图都是矩形,可得这个几何体为三棱柱;
②如图所示,
③这个几何体的侧面积=3×10×4=120cm2;
(2)解$\frac{3}{2}$[(a-$\frac{5}{3}$)x+$\frac{1}{2}$]=1得x=-$\frac{1}{3(a-\frac{5}{3})}$,
解$\frac{1.7-2x}{0.3}$-1=$\frac{0.8+x}{0.6}$得x=$\frac{2}{5}$,
∵方程$\frac{3}{2}$[(a-$\frac{5}{3}$)x+$\frac{1}{2}$]=1和方程$\frac{1.7-2x}{0.3}$-1=$\frac{0.8+x}{0.6}$的解相同,
∴-$\frac{1}{3(a-\frac{5}{3})}$=$\frac{2}{5}$,
∴a=$\frac{5}{2}$.
点评 本题考查了由三视图判断几何体的知识,考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,还考查了同解方程.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
2.1光年大约是9050000000000km,用科学记数法表示为( )km.
| A. | 905×1010 | B. | 90.5×1011 | C. | 9.05×1012 | D. | 0.95×1013 |
3.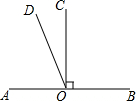 如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )
如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )
 如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )
如图,已知直线AB,线段CO⊥AB于点O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度数为( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
 如图,直线AB与CD相交于E点,EF⊥AB,垂足为E,∠1=125°,则∠2的度数是35°.
如图,直线AB与CD相交于E点,EF⊥AB,垂足为E,∠1=125°,则∠2的度数是35°.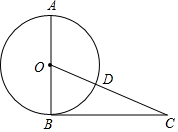 如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,
如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC相交于点D,且CD=2,BC=4,