题目内容
19. 如图,正比例函数y=kx(k≠0)的图象经过点A(2,4),AB⊥x轴于点B,将△ABO绕点A逆时针旋转90°得到△ADC,则直线AC的函数表达式为y=-0.5x+5.
如图,正比例函数y=kx(k≠0)的图象经过点A(2,4),AB⊥x轴于点B,将△ABO绕点A逆时针旋转90°得到△ADC,则直线AC的函数表达式为y=-0.5x+5.
分析 直接把点A(2,4)代入正比例函数y=kx,求出k的值即可;由A(2,4),AB⊥x轴于点B,可得出OB,AB的长,再由△ABO绕点A逆时针旋转90°得到△ADC,由旋转不变性的性质可知DC=OB,AD=AB,故可得出C点坐标,再把C点和A点坐标代入y=ax+b,解出解析式即可.
解答 解:∵正比例函数y=kx(k≠0)经过点A(2,4)
∴4=2k,
解得:k=2,
∴y=2x;
∵A(2,4),AB⊥x轴于点B,
∴OB=2,AB=4,
∵△ABO绕点A逆时针旋转90°得到△ADC,
∴DC=OB=2,AD=AB=4
∴C(6,2)
设直线AC的解析式为y=ax+b,
把(2,4)(6,2)代入解析式可得:$\left\{\begin{array}{l}{2a+b=4}\\{6a+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.5}\\{b=5}\end{array}\right.$,
所以解析式为:y=-0.5x+5
点评 本题考查的是一次函数图象上点的坐标特点及图形旋转的性质,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
7.“五一”旅游黄金周期间,几名同学包租一辆面包车前往某景区游玩,面包车的租价为180元,出发时,又增加了2名学生,结果每个同学比原来少分担3元车费.设参加游玩的同学为x人,则可得方程( )
| A. | $\frac{180}{x}$-$\frac{180}{x+2}$=2 | B. | $\frac{180}{x+2}$-$\frac{180}{x}$=3 | C. | $\frac{180}{x}$-$\frac{180}{x-2}$=3 | D. | $\frac{180}{x-2}$-$\frac{180}{x}$=3 |
14. 如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
 如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
 已知一次函数y=-2x+7的图象与x轴、y轴分别交于点A、B.
已知一次函数y=-2x+7的图象与x轴、y轴分别交于点A、B.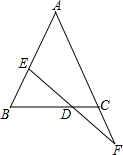 已知:如图,D是EF的中点,BE=CF,求证:△ABC是等腰三角形.
已知:如图,D是EF的中点,BE=CF,求证:△ABC是等腰三角形.