Question

3．如图：边长为a的大正方形中有一个边长为b的小正方形．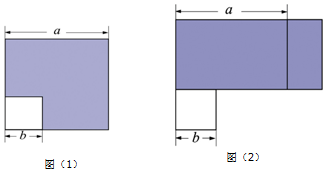

（1）图（1）中阴影部分的面积为a²-b²，图（2）阴影部分面积为（a-b）（a+b）．
（2）通过观察比较两图的阴影部分面积，可以得到乘法公式为a²-b²=（a-b）（a+b）．（用式子表达）
（3）计算：102×98（不用公式计算不得分）

Answer 1

分析 （1）根据正方形的面积公式即可得到结论；
（2）图（1）阴影部分的面积=大正方形的面积-小正方形的面积，图（2）影部分的面积根据矩形面积公式即可得出，根据阴影部分的面积相等可得等式；
（3）计算题直接利用平方差公式即可．

解答 解：（1）图（1）阴影部分的面积a²-b²，图（2）阴影部分的面积（a-b）（a+b）；
故答案为：a²-b²，（a-b）（a+b）；

（2）∵图（1）阴影部分的面积a²-b²，图（2）阴影部分的面积（a-b）（a+b），
则a²-b²=（a-b）（a+b）．
故答案为：a²-b²=（a-b）（a+b）；

（2）102×98
=（100+2）（100-2）
=100²-2²
=10000-4
=9996．

点评 本题利用组合图形考查平方差公式，计算题较为简单，直接利用公式即可．做题时认真观察图形，找到各部分的面积及两面积相等是解决本题的关键．