题目内容
4.分解因式:(1)x2-5x
(2)25x2-81y2
(3)x3-2x2y+xy2
(4)x2(a-1)+y2(1-a)
(5)a4-1
(6)a4-18a2+81.
分析 (1)直接提取公因式x即可;
(2)利用平方差公式分解因式;
(3)此多项式有公因式,应先提取公因式,再对余下的多项式进行观察,有3项,可采用完全平方公式继续分解;
(4)先提取公因式(a-1),再对余下的多项式利用平方差公式继续分解;
(5)两次利用平方差公式分解因式;
(6)先利用完全平方公式分解因式,再利用平方差公式分解因式.
解答 解:(1)x2-5x=x(x-5);
(2)25x2-81y2=(5x+9y)(5x-9y);
(3)x3-2x2y+xy2
=x(x2-2xy+y2)
=x(x-y)2;
(4)x2(a-1)+y2(1-a)
=(a-1)(x2-y2)
=(a-1)(x+y)(x-y);
(5)a4-1
=(a2+1)(a2-1)
=(a2+1)(a+1)(a-1);
(6)a4-18a2+81
=(a2-9)2
=(a+3)2(a-3)2.
点评 本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.某鞋店试销一种新款女鞋,试销期间五种型号的该款鞋卖出情况如表:
鞋店经理最关心的是哪种型号的鞋畅销,则他最关心的统计量应是( )
| 型号 | A | B | C | D | E |
| 数量(双) | 3 | 8 | 22 | 10 | 4 |
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
16.已知同一平面内A、B、C三点,线段AB=6cm,BC=2cm,则A、C两点间的距离是( )
| A. | 8cm | B. | 84m | C. | 8cm或4cm | D. | 无法确定 |
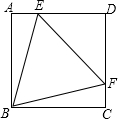 如图,正方形ABCD中,点E、F分别在AD、DC上,且△BEF为等边三角形.下列结论:①DE=DF;②∠AEB=75°;③AE+CF=EF;④BE=$\sqrt{2}$DE;⑤△EDF与△BFC的面积比为2:1.其中正确的结论有4个.
如图,正方形ABCD中,点E、F分别在AD、DC上,且△BEF为等边三角形.下列结论:①DE=DF;②∠AEB=75°;③AE+CF=EF;④BE=$\sqrt{2}$DE;⑤△EDF与△BFC的面积比为2:1.其中正确的结论有4个.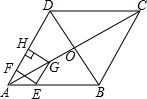 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒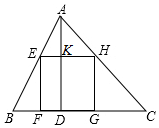 若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc
若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc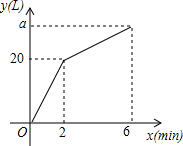 一个容器装有一个注水管和两个排水管,每个排水管每分钟排水7.5L,从某一时刻开始2min内只注水不排水,2min后开启一个排水管,容器内的水量y(L)与注水时间x(min)之间的函数关系如图所示.
一个容器装有一个注水管和两个排水管,每个排水管每分钟排水7.5L,从某一时刻开始2min内只注水不排水,2min后开启一个排水管,容器内的水量y(L)与注水时间x(min)之间的函数关系如图所示.