题目内容
18.已知关于x的方程(m+$\sqrt{3}$)${x}^{{m}^{2}-1}$+2(m+3)x-5=0.(1)当方程是一元二次方程时,求m的值;
(2)当方程是一元一次方程时,求m的值.
分析 (1)根据一元二次方程的定义得到:m2-1=2且m+$\sqrt{3}$≠0,由此可以求得m的值;
(2)由一元一次方程的定义得到:①m+$\sqrt{3}$=0且2(m+3)≠0;②m2-1=1且m+$\sqrt{3}$+2(m+3)≠0;③m2-1=0且2(m+3)≠0;由此可以求得m的值.
解答 解:(1)∵关于x的方程(m+$\sqrt{3}$)${x}^{{m}^{2}-1}$+2(m+3)x-5=0,是一元二次方程,
∴m2-1=2且m+$\sqrt{3}$≠0,
解得m=$\sqrt{3}$;
(2)∵关于x的方程(m+$\sqrt{3}$)${x}^{{m}^{2}-1}$+2(m+3)x-5=0是一元一次方程,
∴①m+$\sqrt{3}$=0且2(m+3)≠0,
解得m=-$\sqrt{3}$;
②m2-1=1且m+$\sqrt{3}$+2(m+3)≠0,
解得m=±$\sqrt{2}$;
③m2-1=0且2(m+3)≠0,
解得m=±1.
点评 本题考查了一元二次方程、一元一次方程的定义.注意,一元一次方程的未知数的系数不等于零,一元二次方程的二次项系数不等于零.

练习册系列答案
相关题目
 中国象棋棋盘中蕴含着平面直角坐标系.如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图中的“马”可以从它所在的位置直接走到点A、点B或点C处.
中国象棋棋盘中蕴含着平面直角坐标系.如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图中的“马”可以从它所在的位置直接走到点A、点B或点C处.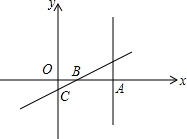 已知,直线x=2与x轴相交于点A,动直线y=0.5x+b分别与x轴,y轴相交于点B、C,点D在直线x=2上.
已知,直线x=2与x轴相交于点A,动直线y=0.5x+b分别与x轴,y轴相交于点B、C,点D在直线x=2上.