题目内容
10.点P在线段AB上,AP2=AB•PB,若PB=4,求AP的长.分析 根据黄金分割的定义易得点P为AB的黄金分割点,则AP=$\frac{\sqrt{5}-1}{2}$AB,所以PB=AB-AP=$\frac{3-\sqrt{5}}{2}$AB,依此可得PB,AP的关系,列式计算可得AP的长.
解答 解:∵点P在线段AB上,AP2=AB•PB,
∴AP=$\frac{\sqrt{5}-1}{2}$AB,
∴PB=AB-AP=$\frac{3-\sqrt{5}}{2}$AB,
∴AP=$\frac{\frac{\sqrt{5}-1}{2}}{\frac{3-\sqrt{5}}{2}}$PB=2$\sqrt{5}$+2.
故AP的长是2$\sqrt{5}$+2.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=$\frac{\sqrt{5}-1}{2}$AB,并且线段AB的黄金分割点有两个.

练习册系列答案
相关题目
2.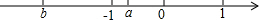 有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )
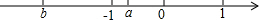 有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )| A. | a+b<0 | B. | a-b<0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
5.若方程2x2-4x-k=0有两个相等的实数根,则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
 如图,DE是△ABC的中位线,DE=2cm,AB+AC=12cm,则△ABC的周长是16cm.
如图,DE是△ABC的中位线,DE=2cm,AB+AC=12cm,则△ABC的周长是16cm.