题目内容
13.对于一元二次方程ax2+bx+c=0(a≠0),且(a-2)2+|b-4|+$\sqrt{c-6}$=0.写出这个一元二次方程.分析 首先利用非负数的性质求得a、b、c的值,然后将其代入关于x的一元二次方程ax2+bx+c=0即可求解.
解答 解:∵(a-2)2+|b-4|+$\sqrt{c-6}$=0,
∴a-2=0,解得a=2,
b-4=0,解得b=4,
$\sqrt{c-6}$=0,解得c=6.
故这个一元二次方程是2x2+4x+6=0.
点评 本题综合考查了非负数的性质和一元二次方程的定义,解题的关键是根据非负数的性质求得a、b、c的值.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.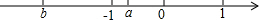 有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )
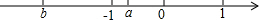 有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论中,错误的是( )| A. | a+b<0 | B. | a-b<0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
5.若方程2x2-4x-k=0有两个相等的实数根,则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
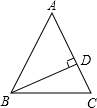 如图,在△ABC中,AB=AC,BD⊥AC,D是垂足,DC=4,cosA=$\frac{3}{5}$,求tanC的值.
如图,在△ABC中,AB=AC,BD⊥AC,D是垂足,DC=4,cosA=$\frac{3}{5}$,求tanC的值. 如图,同一数轴上四点A,B,C,D所对应的数分别为a,b,c,d,且要邻两刻度的距离表示单位长度,若3a-2b=0,则数轴上点c对应的数为2,a+b-c-d=5.
如图,同一数轴上四点A,B,C,D所对应的数分别为a,b,c,d,且要邻两刻度的距离表示单位长度,若3a-2b=0,则数轴上点c对应的数为2,a+b-c-d=5.