题目内容
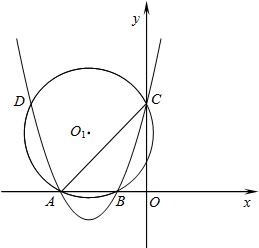 抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.(1)求抛物线的解析式;
(2)求⊙O1的半径;
(3)在抛物线的对称轴上是否存在点P使PB+PC最小?若存在,请写出P点坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法求出抛物线的解析式;
(2)如图所示,由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度;
(3)根据抛物线的解析式可确定C点坐标为(0,3),再利用待定系数法确定直线AC的关系式为y=x+3,由于使得PB+PC的值最小的点P为直线AC与对称轴的交点,把x=-2代入y=x+3即可确定P点坐标.
(2)如图所示,由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度;
(3)根据抛物线的解析式可确定C点坐标为(0,3),再利用待定系数法确定直线AC的关系式为y=x+3,由于使得PB+PC的值最小的点P为直线AC与对称轴的交点,把x=-2代入y=x+3即可确定P点坐标.
解答: 解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),
解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),
∴
,
解得a=1,b=4.
∴抛物线的解析式为:y=x2+4x+3;
(2)由(1)知,抛物线解析式为y=x2+4x+3,
∵令x=0,得y=3,
∴C(0,3),
∴OC=OA=3,则△AOC为等腰直角三角形,∠BAC=45°
如图所示,连接O1B、O1B,则∠BO1C=2∠BAC=90°.
在Rt△BOC中,由勾股定理得:BC=
=
,
在等腰Rt△BO1C中,⊙O1的半径O1B=BCsin45°=
×
=
;
(3)作抛物线的对称轴l,交AC于P,则P点即为所求.
(∵B点关于l的对称点是A,∴P点即是在l上使PB+PC最小的点.该理由不写亦可)
∵P点在对称轴l上,
∴P点的横坐标为-
=-2.
设直线AC的函数表达式为y=kx+t(k≠0).
∵由A(-3,0),C(0,3),
∴
,
解得
.
∴直线AC的函数表达式为y=x+3.
将x=-2代入y=x+3,得y=1.
∴P点的坐标为(-2,1).
 解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),
解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),∴
|
解得a=1,b=4.
∴抛物线的解析式为:y=x2+4x+3;
(2)由(1)知,抛物线解析式为y=x2+4x+3,
∵令x=0,得y=3,
∴C(0,3),
∴OC=OA=3,则△AOC为等腰直角三角形,∠BAC=45°
如图所示,连接O1B、O1B,则∠BO1C=2∠BAC=90°.
在Rt△BOC中,由勾股定理得:BC=
| 12+32 |
| 10 |
在等腰Rt△BO1C中,⊙O1的半径O1B=BCsin45°=
| 10 |
| ||
| 2 |
| 5 |
(3)作抛物线的对称轴l,交AC于P,则P点即为所求.
(∵B点关于l的对称点是A,∴P点即是在l上使PB+PC最小的点.该理由不写亦可)
∵P点在对称轴l上,
∴P点的横坐标为-
| 4 |
| 2 |
设直线AC的函数表达式为y=kx+t(k≠0).
∵由A(-3,0),C(0,3),
∴
|
解得
|
∴直线AC的函数表达式为y=x+3.
将x=-2代入y=x+3,得y=1.
∴P点的坐标为(-2,1).
点评:本题综合考查了二次函数的图象与性质、待定系数法求函数解析式、圆的性质等重要知识点,涉及的考点较多,试题难度较大.(3)题的关键点是确定点P的位置.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
下列各式能用平方差公式计算的是( )
| A、(2a+b)(2b-a) |
| B、(x+1)(-x-1) |
| C、(-m-n)(-m+n) |
| D、(3x-y)(-3x+y) |
下列数中,绝对值最大的是( )
A、
| ||
| B、0 | ||
| C、-2 | ||
| D、-1 |
下列命题是假命题的是( )
| A、同旁内角互补 |
| B、垂直于同一条直线的两条直线平行 |
| C、对顶角相等 |
| D、同角的余角相等 |
已知|a-6|+
+(c-10)2=0,则这个三角形的形状是( )
| b-8 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 如图,过y轴上点A的一次函数y=ax+b与反比例函数y=
如图,过y轴上点A的一次函数y=ax+b与反比例函数y=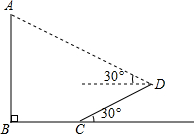 已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知
已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知