题目内容
1.将抛物线y=(x+1)2向下平移2个单位,得到新抛物线的函数解析式是y=(x+1)2-2.分析 先由二次函数的性质得到抛物线y=(x+1)2的顶点坐标为(-1,0),再根据点平移的规律,点(-1,0)平移后所得对应点的坐标为(-1,-2),然后根据顶点式写出平移后的抛物线的解析式.
解答 解:抛物线y=(x+1)2的顶点坐标为(-1,0),把(-1,0)向下平移2个单位所得对应点的坐标为(-1,-2),所以平移后的抛物线的解析式是y=(x+1)2-2.
故答案为y=(x+1)2-2.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
11.小明周一到周五的每天下午16:00放学,这时钟面上时针与分针夹角的度数为( )
| A. | 130° | B. | 120° | C. | 160° | D. | 100° |
9.在不透明的盒子中装有3个红球,2个白球,它们除颜色外均相同,则从盒中子任意摸出一个球是白球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16.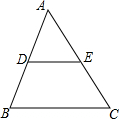 如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
 如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )| A. | AD:AB=DE:BC | B. | AD:DB=DE:BC | C. | AD:DB=AE:EC | D. | AE:AC=AD:DB |
11.下列各组线段,能组成三角形的是( )
| A. | 2cm 3cm 5cm | B. | 5cm 6cm 10cm | C. | 2cm 2cm 5cm | D. | 3cm 4cm 8cm |
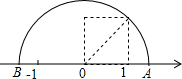 如图,正方形的边长是一个单位长度,则图中A点所表示的数是$\sqrt{2}$,在本题的解答过程,运用了一种重要的数学思想,这种数学思想是数形结合思想.
如图,正方形的边长是一个单位长度,则图中A点所表示的数是$\sqrt{2}$,在本题的解答过程,运用了一种重要的数学思想,这种数学思想是数形结合思想.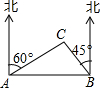 世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.
世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.