题目内容
3.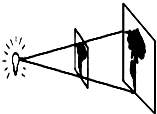 如图,用投影仪将图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为18cm.
如图,用投影仪将图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为18cm.
分析 如图,PC=20,PD=60,AB=6,证明△PAB∽△AEF,则利用相似三角形的性质得到$\frac{6}{EF}$=$\frac{20}{60}$,然后利用比例性质求EF即可.
解答 解: 如图,
如图,
PC=20,PD=60,AB=6,
∵AB∥EF,
∴△PAB∽△AEF,
∴$\frac{AB}{EF}$=$\frac{PC}{PD}$,即$\frac{6}{EF}$=$\frac{20}{60}$,
∴EF=18(cm).
故答案为18.
点评 本题考查了相似三角形的应用:从实物图中抽象出几何图形,然后利用相似三角形的性质求解.

练习册系列答案
相关题目
15.使$\sqrt{3x-1}$有意义的x的取值范围是( )
| A. | x≥$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x>-$\frac{1}{3}$ | D. | x≥-$\frac{1}{3}$ |
11.下列二次根式是最简二次根式的是( )
| A. | 2$\sqrt{a}$ | B. | $\sqrt{8{x}^{2}}$ | C. | $\sqrt{{y}^{3}}$ | D. | $\sqrt{\frac{b}{4}}$ |
12.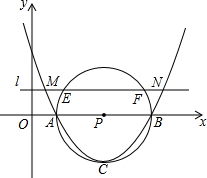 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{2}$ | C. | 5 | D. | 6 |
 如图:P是?ABCD的边AD的中点,且PB=PC.求证:四边形ABCD是矩形.
如图:P是?ABCD的边AD的中点,且PB=PC.求证:四边形ABCD是矩形. 如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=48°,则∠BDF=84°.
如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=48°,则∠BDF=84°.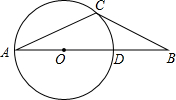 如图,在△ABC中,2∠A+∠B=90°,点0在AB边上,以O点为圆心的圆经过A、C 两点,交AB于D点.
如图,在△ABC中,2∠A+∠B=90°,点0在AB边上,以O点为圆心的圆经过A、C 两点,交AB于D点.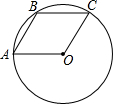 如图,⊙O经过?OABC的顶点A、B、C,若OA=3,则$\widehat{AB}$的长为π(结果保留π).
如图,⊙O经过?OABC的顶点A、B、C,若OA=3,则$\widehat{AB}$的长为π(结果保留π).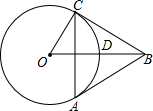 如图,⊙O的半径为2,OB=4,OB交⊙O于点D,点C是⊙O上一动点,以BC为边向下作等边△ABC.
如图,⊙O的半径为2,OB=4,OB交⊙O于点D,点C是⊙O上一动点,以BC为边向下作等边△ABC.