题目内容
16. 如图:P是?ABCD的边AD的中点,且PB=PC.求证:四边形ABCD是矩形.
如图:P是?ABCD的边AD的中点,且PB=PC.求证:四边形ABCD是矩形.
分析 根据平行四边形性质得出AB=DC,AB∥DC,推出∠D+∠A=180°,根据SSS证△ABP≌△DCP,推出∠D=∠A,求出∠D=90°,根据矩形的判定推出即可.
解答  证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠D+∠A=180°,
∵P是DA边的中点,
∴AP=PD,
在△ABP和△DCP中
∵$\left\{\begin{array}{l}{AP=DP}\\{AB=DC}\\{BP=PC}\end{array}\right.$,
∴△ABP≌△DCP(SSS),
∴∠D=∠A,
∵∠D+∠A=180°,
∴∠D=∠A=90°,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
点评 本题考查了全等三角形的性质和判定,平行四边形的性质,矩形的判定的应用,注意:有一个角是直角的平行四边形是矩形.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.计算(-6)÷(-1)的结果等于( )
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | -7 |
8.一只蚂蚁沿数轴从点A向右直爬15个单位到达点B,点B表示的数为-2,则点A所表示的数为( )
| A. | 15 | B. | 13 | C. | -13 | D. | -17 |
 如图,泰山与青岛之间的某一列车,运行途中停靠的车站是:泰山、济南、淄博、潍坊、青岛,那么要为这一列车制作的火车票共有20种.
如图,泰山与青岛之间的某一列车,运行途中停靠的车站是:泰山、济南、淄博、潍坊、青岛,那么要为这一列车制作的火车票共有20种.




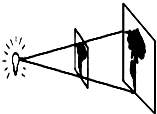 如图,用投影仪将图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为18cm.
如图,用投影仪将图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为18cm.