题目内容
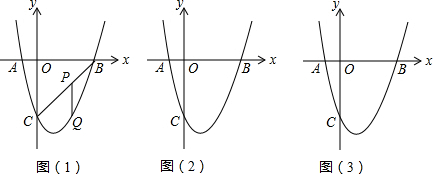
5.如图(1),抛物线y=x2-2x+k与x轴交于A、B两点.与y轴交于点C(0,-3)(1)如图(1),P为线段BC上的动点.过P作x轴的垂线,交抛物线与Q点.求PQ长度的最值.
(2)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(3)在抛物线y=x2-2x+k上求点Q,使△BCQ是以BC为直角边的直角三角形.
分析 (1)用待定系数法先确定出抛物线解析式,再建立PQ函数解析式即可得出PQ极值;
(2)先建立S四边形ABDC=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{75}{8}$,函数关系式,即可确定出点D坐标;
(3)分两种情况用直线函数解析式和抛物线解析式联立即可确定出点D的坐标.
解答 解:(1)∵抛物线y=x2-2x+k与x轴交于A、B两点.与y轴交于点C(0,-3),
∴k=-3,
∴抛物线解析式为y=x2-2x-3,
∴A(-1,0),B(3,0),C(0,-3),
∴直线BC解析式为y=x-3,
设P(m,m-3)(0≤m≤3),
∴Q(m,m2-2m-3),
∴PQ=m-3-(m2-2m-3)=-m2+3m=(m-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴当m=$\frac{3}{2}$时,PQ长度的最大值为$\frac{9}{4}$,当m=0或m=3时,PQ长度的最小值为0;
(2)如图2,∵A(-1,0),B(3,0),C(0,-3),
∴AB=4,OC=3,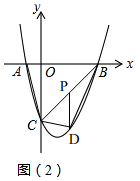 设P(m,m-3)(0≤m≤3),
设P(m,m-3)(0≤m≤3),
∴D(m,m2-2m-3),
∴PD=m-3-(m2-2m-3)=-m2+3m,
∴S四边形ABDC=S△ABC+S△CDP+S△BDP=$\frac{1}{2}$AB×OC+$\frac{1}{2}$PD×|xB|=$\frac{1}{2}$×4×3+$\frac{1}{2}$×(-m2+3m)×3=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{75}{8}$,
∴当m=$\frac{3}{2}$时,S四边形ABDC最大=$\frac{75}{8}$,此时,点D($\frac{3}{2}$,-$\frac{15}{4}$);
(3)由(1)知,直线BC解析式为y=x-3,
∵△BCQ是以BC为直角边的直角三角形.
∴BQ⊥BC或CQ⊥BC,
当BQ⊥BC时,直线BQ的解析式为y=-x+3①,
由(1)知,抛物线解析式为y=x2-2x-3②,
联立①②得,Q(-2,5),
当CQ⊥BC时,直线CQ的解析式为y=-x-3③,
联立②③得,Q(1,-4),
∴满足条件的点P的坐标为(-2,5)或(1,-4).
点评 此题是二次函数综合题,主要考查了待定系数法,三角形面积公式,直角三角形的性质,解本题的关键是建立函数解析式,是一道比较简单中考常考题.

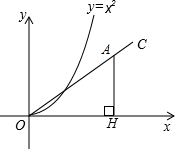 如图,射线OC,与x轴的夹角为30o,在射线OC上取一点A,过点A作AH⊥x轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的个数是( )
如图,射线OC,与x轴的夹角为30o,在射线OC上取一点A,过点A作AH⊥x轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的个数是( )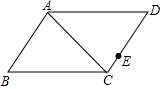 如图,在?ABCD中,AB=6cm,BC=10cm,AC=8cm,E是CD上的点,DE=2CE,点P以1cm/s的速度由点D向点A移动,则当△EDP为等腰三角形且DP≠DE时,运动时间t为$\frac{10}{3}$或4.8s.
如图,在?ABCD中,AB=6cm,BC=10cm,AC=8cm,E是CD上的点,DE=2CE,点P以1cm/s的速度由点D向点A移动,则当△EDP为等腰三角形且DP≠DE时,运动时间t为$\frac{10}{3}$或4.8s.