题目内容
13.若二元一次方程组$\left\{\begin{array}{l}{2x+5y=-26}\\{ax-by=-4}\end{array}\right.$和$\left\{\begin{array}{l}{3x-5y=36}\\{bx+ay=-8}\end{array}\right.$有相同的解.求(2a+b)2017的值.分析 联立不含a与b的方程组成方程组,求出解得到x与y的值,代入剩下方程求出a与b的值,即可求出原式的值.
解答 解:联立得:$\left\{\begin{array}{l}{2x+5y=-26①}\\{3x-5y=36②}\end{array}\right.$,
①+②得:5x=10,即x=2,
把x=2代入①得:y=-6,
把x=2,y=-6代入得:$\left\{\begin{array}{l}{a+3b=-2}\\{-3a+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
则原式=1.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
3.古代有这样一个寓言故事:驴子和骡子一同走,它们驮着不同袋数的货物,每袋货物都是一样重的.驴子抱怨负担太重,骡子说:“你抱怨干嘛,如果你给我一袋,那我所负担的就是你的两倍;如果我给你一袋,我们才恰好驮的一样多!”如果设驴子驮的袋数为x袋,骡子驮的袋数为y袋,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{y+1}{2}=(x-1)}\\{y+1=x-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y+1=\frac{1}{2}(x-1)}\\{y-1=x+1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y+1=2(x-1)}\\{y-1=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+1=2(x-1)}\\{y+1=x-1}\end{array}\right.$ |
 如图,△ABD≌△DEF,CE=6,FC=2,则BC=8.
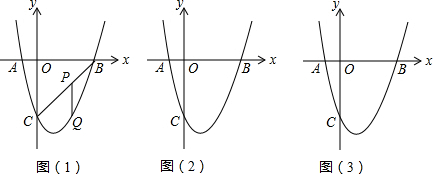
如图,△ABD≌△DEF,CE=6,FC=2,则BC=8.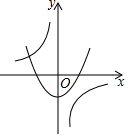 如图,反比例函数y1=$\frac{k}{x}$的图象与以y轴为对称轴的二次函数y2=ax2+bx+c的图象交于点A,则函数y=ax2+(b-k)x+c的图象可能是( )
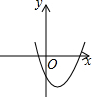
如图,反比例函数y1=$\frac{k}{x}$的图象与以y轴为对称轴的二次函数y2=ax2+bx+c的图象交于点A,则函数y=ax2+(b-k)x+c的图象可能是( )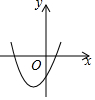

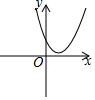
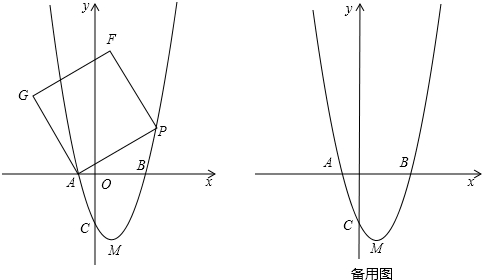
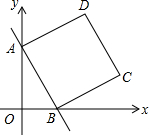 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴和y轴分别交于点B和点A,以AB为边在第一象限内作正方形ABCD.
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴和y轴分别交于点B和点A,以AB为边在第一象限内作正方形ABCD.