题目内容
12. 已知△ABC中,∠A=25°,∠B=40°.
已知△ABC中,∠A=25°,∠B=40°.(1)求作:⊙O,使得⊙O是△ABC的外接圆(要求尺规作图,保留作图痕迹,不必写作法)
(2)综合应用:在你所作的圆中,求∠AOB的度数.
分析 (1)分别作边AB、AC的垂直平分线GH、EF,交点即是外接圆的圆心,半径为OA;
(2)利用圆内接四边形对角互补求出∠ADB的度数,根据同弧所对的圆心角是圆周角的二倍可得结论.
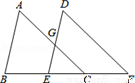
解答  解:(1)如右图:
解:(1)如右图:
作法:分别作边AB、AC的垂直平分线GH、EF,交于点O,以O为圆心,
以OA为半径的圆就是△ABC的外接圆.
(2)在优弧AB上取一点D,连接DA,DB,
∵∠CAB=25°,∠CBA=40°,
∴∠C=180°-∠CAB-∠CBA=115°,
∵四边形CADB是圆的内接四边形,
∴∠ADB=180°-∠ACB=180°-115°=65°,
∴∠AOB=2∠ADB=130°.
点评 本题考查了三角形的外接圆的作法,三角形外接圆的圆心叫外心,是三边垂直平分线的交点,在圆中求角的度数时,经常运用:①同弧所对的圆心角是圆周角的二倍,②圆内接四边形对角互补;要熟练掌握.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
4.对于二次函数y=-3(x-8)2+2,下列说法中,正确的是( )
| A. | 开口向上,顶点坐标为(8,2) | B. | 开口向下,顶点坐标为(8,2) | ||
| C. | 开口向上,顶点坐标为(-8,2) | D. | 开口向下,顶点坐标为(-8,2) |
16.南宁市气象站记录,南宁市建国以来最高气温高达40℃,最低气温为-2℃,那么建国以来南宁市的最高气温比最低气温高( )
| A. | 38℃ | B. | 42℃ | C. | -38℃ | D. | -42℃ |
3.关于x的方程(a-5)x2-4x-1=0有实数根,则a满足( )
| A. | a≥1 | B. | a>1且 a≠5 | C. | a≥1且 a≠5 | D. | a≠5 |

 在期中测试中,我们计算过三边分别为AB=8,BC=5,AC=7的△ABC的内切圆的半径,如图,⊙O是△ABC的外接圆.AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.
在期中测试中,我们计算过三边分别为AB=8,BC=5,AC=7的△ABC的内切圆的半径,如图,⊙O是△ABC的外接圆.AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.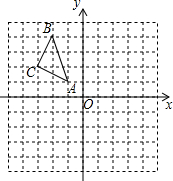 如图,A(-1,1),B(-2,4),C(-3,2).
如图,A(-1,1),B(-2,4),C(-3,2).