题目内容
1. 在期中测试中,我们计算过三边分别为AB=8,BC=5,AC=7的△ABC的内切圆的半径,如图,⊙O是△ABC的外接圆.AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.
在期中测试中,我们计算过三边分别为AB=8,BC=5,AC=7的△ABC的内切圆的半径,如图,⊙O是△ABC的外接圆.AD为直径,连接BD,则AD=$\frac{14\sqrt{3}}{3}$.
分析 作AE⊥BC于E,根据勾股定理求出BE、AE,根据相似三角形的判定定理得到△ABD∽△AEC,根据相似三角形的性质得到比例式,计算即可.
解答 解:作AE⊥BC于E,
设BE=x,则CE=5-x,
由勾股定理得,82-x2=72-(5-x)2,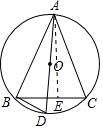
解得,x=4,
则AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=4$\sqrt{3}$,
∵AD为直径,AE⊥BC,
∴∠ABD=∠AEC=90°,又∠D=∠C,
∴△ABD∽△AEC,
∴$\frac{AB}{AE}$=$\frac{AE}{AC}$,即$\frac{8}{4\sqrt{3}}$=$\frac{AD}{7}$,
解得,AD=$\frac{14\sqrt{3}}{3}$,
故答案为:$\frac{14\sqrt{3}}{3}$.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
13.二次函数y=2x2+4x-3的图象的顶点坐标是( )
| A. | (0,-3) | B. | (1,3) | C. | (-1,-3) | D. | (-1,-5) |
12.某商人一次卖出两件衣服,一件赚了百分之15,一件亏了百分之15,售价都是9775元,在这次生意中,该商人( )
| A. | 不赚不赔 | B. | 赚了490元 | C. | 亏了450元 | D. | 亏了490元 |
9.关于函数y=-2x+1,下列结论正确的是( )
| A. | 图象必经过点(-2,1) | B. | y随x的增大而增大 | ||
| C. | 当x>$\frac{1}{2}$时,y<0 | D. | 图象不经过第一象限 |
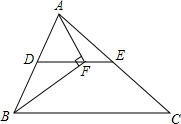 如图,在△ABC中BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=12,BC=16,则线段EF的长为2.
如图,在△ABC中BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=12,BC=16,则线段EF的长为2. 已知△ABC中,∠A=25°,∠B=40°.
已知△ABC中,∠A=25°,∠B=40°. 已知y关于x的二次函数y=x2+2mx-3m2(m≠0)的图象的顶点为A,与x轴交于点B,C,与y轴交于点D.
已知y关于x的二次函数y=x2+2mx-3m2(m≠0)的图象的顶点为A,与x轴交于点B,C,与y轴交于点D.