Question

19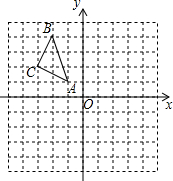．如图，A（-1，1），B（-2，4），C（-3，2）．
（1）画出△ABC关于原点O对称的△A₁B₁C₁；
（2）若将△ABC绕点C顺时针方向旋转90°后，求AC边扫过的图形的面积．

Answer 1

分析 （1）利用关于原点对称的点的坐标特征写出A₁、B₁、C₁的坐标，然后描点即可；
（2）利用弧长公式求解．

解答 解：（1）如图，△A₁B₁C₁为所作；

（2）AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
所以AC边扫过的图形的面积=$\frac{90•π•\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π．

点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．