题目内容
2．若点P的坐标是（2，1），则点P在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 根据各象限内点的坐标特征解答．
解答 解：点P（2，1）在第一象限．
故选A．
点评 本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
12．
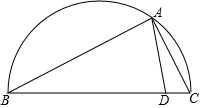如图，以BC为直径的半圆中，A为弧BC上一点，AC=$\sqrt{3}$，AB=4，D为BC上一点，∠CAD=30°，则AD的长为（ ）
如图，以BC为直径的半圆中，A为弧BC上一点，AC=$\sqrt{3}$，AB=4，D为BC上一点，∠CAD=30°，则AD的长为（ ）| A． | $\frac{9}{5}$ | B． | $\frac{8}{5}$ | C． | $\frac{7}{5}$ | D． | $\frac{6}{5}$ |
13．下列运算正确的是（ ）
| A． | x3+x3=2x6 | B． | （x2）3=x5 | C． | x6÷x2=x3 | D． | x2•x3=x5 |
10．已知点P（a，2），Q（-1，b）关于x轴对称，则点（a，b）位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
17．下列化简正确的是（ ）
| A． | 2a+3b=5ab | B． | 7ab-3ab=4 | C． | 2ab+3ab=5ab | D． | a2+a2=a4 |
7．如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A瞬时针旋转到位置①可得到点P1，此时AP1=$\sqrt{2}$；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=$\sqrt{2}$+1；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=$\sqrt{2}$+2；…，按此规律继续旋转，直至得到点P2017为止，则AP2017长为（ ）
| A． | 1344+672$\sqrt{2}$ | B． | 1344+673$\sqrt{2}$ | C． | 1345+673$\sqrt{2}$ | D． | 1345+674$\sqrt{2}$ |
14．在Rt△ABC中，∠C=90°，AB=6，cosB=$\frac{2}{3}$，则BC的长为（ ）
| A． | $\sqrt{5}$ | B． | 4 | C． | 2$\sqrt{5}$ | D． | 5 |
11．若方程组$\left\{\begin{array}{l}{x+y=a}\\{x-y=4a}\end{array}\right.$的解是二元一次方程3x-5y-90=0的一个解，则a的值是（ ）
| A． | 3 | B． | 2 | C． | 6 | D． | 7 |
12．
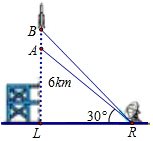如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于地面R处的雷达站观测得知AR的距离是6km，仰角∠ARL=30°，又经过1s后火箭到达B点，此时测得仰角∠BRL=45°，则这枚火箭从A到B的平均速度为（ ）km/s．
如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于地面R处的雷达站观测得知AR的距离是6km，仰角∠ARL=30°，又经过1s后火箭到达B点，此时测得仰角∠BRL=45°，则这枚火箭从A到B的平均速度为（ ）km/s．| A． | 3$\sqrt{3}$-3 | B． | 3$\sqrt{3}$ | C． | 3$\sqrt{3}$+3 | D． | 3 |