题目内容
7. 如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于( )
如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于( )| A. | 24° | B. | 30° | C. | 32° | D. | 42° |
分析 根据角平分线定义求出∠ABP=∠CBP,根据线段的垂直平分线性质得出BP=CP,求出∠CBP=∠BCP,根据三角形内角和定理得出方程3∠ABP+24°+60°=180°,求出方程的解即可.
解答 解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
解得:∠ABP=32°,
故选:C.
点评 本题考查了三角形内角和定理,线段垂直平分线性质,等腰三角形的性质的应用,能求出∠ABP=∠CBP=∠BCP是解此题的关键,数形结合思想的应用.

练习册系列答案
相关题目
18.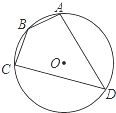 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则弧AC的长( )| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | 4π |
19.本学期的四次数学单元练习中,甲、乙两位同学的平均成绩一样,方差分别为1.0,0.6,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 甲乙两人的成绩一样稳定 | ||
| C. | 乙比甲的成绩稳定 | D. | 无法确定谁的成绩更稳定 |
16.某班5名同学在一周内参加家务劳动的时间如表所示,则关于“劳动时间”的这组数据的中位数是4.
| 劳动时间(小时) | 2 | 3 | 4 | 5 |
| 人数 | 1 | 1 | 2 | 1 |
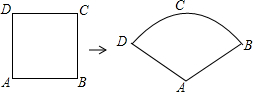 如图,将边长为2的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为( )
如图,将边长为2的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为( ) 已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的作直线EF⊥BD分别交AD,BC于E,F两点,连结BE,DF.求证:四边形BFDE为菱形.
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的作直线EF⊥BD分别交AD,BC于E,F两点,连结BE,DF.求证:四边形BFDE为菱形.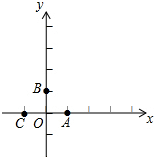 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是(2,0),点P2016的坐标为(0,0).
如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是(2,0),点P2016的坐标为(0,0).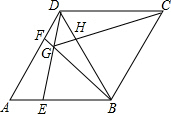 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: