题目内容
正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )
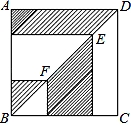
A.a2 B.0.25a2 C.0.5a2 D.2
C【考点】轴对称的性质.
【分析】只要证明图中的阴影部分与对应的非阴影部分全等,则图中阴影部分的面积就不难计算了.
【解答】解:如图,

∵FH∥CD,
∴∠BHF=∠C=90°(同位角相等);
在△BFH和△BDC中,

∴△BFH∽△BDC(AA),
∴
同理,得
又∵AD=CD,
∴GF=FH,
∵∠BGF=∠BHF=90°,BF=BF,
∴△BGF≌△BHF,
∴S△BGF=S△BHF,
同理,求得多边形GFEJ与多边形HFEI的面积相等,多边形JEDA与多边形IEDC的面积相等,
∴图中阴影部分的面积是正方形ABCD面积的一半, .
.
故选:C.
【点评】考查了轴对称的性质,解答本题时主要运用了正方形的性质,相似三角形的判定以及相似三角形的性质.所以,在以后的解题中合理的利用已学的定理与性质会降低题的难度.

练习册系列答案
相关题目

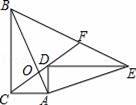

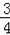
 x+3与x轴y轴分别交于点A、点B,抛物线y=﹣
x+3与x轴y轴分别交于点A、点B,抛物线y=﹣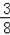




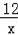
 C.y=
C.y=
 D.y=
D.y=
