题目内容
已知:直线y=﹣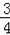
 x+3与x轴y轴分别交于点A、点B,抛物线y=﹣
x+3与x轴y轴分别交于点A、点B,抛物线y=﹣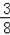
 x2+bx+c经过点A和点B.
x2+bx+c经过点A和点B.
(1)求抛物线的解析式;
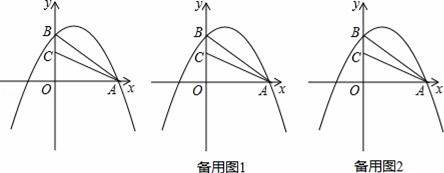
(2)点C(0,2),点P(m,0)是线段OA上的一点(不与O、A重合),过点P作PM垂直x轴,交抛物线于点M,连接BM、AC、AM,设四边形ACBM的面积为S,求S与m的函数关系式(不要求写出自变量的取值范围);
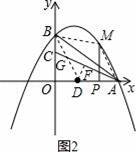
(3)在(2)的条件下,点D是线段OP的中点,连接BD,当S取最大值时,试求直线BD与AC所成的锐角度数.

【考点】二次函数综合题.
【分析】(1)根据一次函数解析式求出A、B坐标,代入二次函数解析式即可求出二次函数解析式;
(2)根据题意作出辅助线,根据S=S梯形OPMB﹣+S△APM﹣S△OAC可得函数解析式;
(3))由(2)中函数关系式得出m及S的值,根据点D是线段OP的中点得出D点坐标,利用待定系数法求出直线AC、BD的解析式,故可得出G点坐标,利用两点间的距离公式求出DG的长,过点D作DF⊥AC于点F,求出直线DF的解析式,故可得出F点的坐标,求出DF的长,利用锐角三角函数的定义即可得出结论.
【解答】解:(1)在y=﹣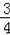
 x+3中,
x+3中,
当y=0时,x=4,所以A(4,0),
当x=0时,y=3,所以B(0,3),
∵抛物线y=﹣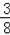
 x2+bx+c经过A、B,
x2+bx+c经过A、B,
∴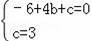
 ,解得
,解得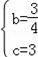
 ,
,
∴抛物线的解析式为:y=﹣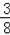
 x2+
x2+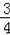
 x+3;
x+3;
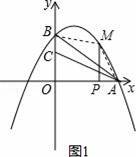
(2)如图1所示,
∵P(m,0),
∴OP=m,PM=﹣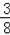
 m2+
m2+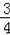
 m+3
m+3
∴S=S梯形OPMB+S△APM﹣S△OAC
=
 (PM+OB)•OP+
(PM+OB)•OP+
 AP•PM﹣
AP•PM﹣
 OA•OC
OA•OC
=
 (﹣
(﹣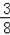
 m2+
m2+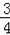
 m+3+3)•m+
m+3+3)•m+
 (4﹣m)(﹣
(4﹣m)(﹣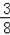
 m2+
m2+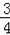
 m+3)﹣
m+3)﹣
 ×4×2
×4×2
=﹣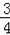
 m2+3m+2(0<m<4);
m2+3m+2(0<m<4);
(3)∵由(2)知S=﹣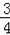
 m2+3m+2,
m2+3m+2,
∴当m=2时,S最大=5,
∴P(2,0).
∵点D是线段OP的中点,
∴D(1,0).
设直线AC的解析式为y=kx+b(k≠0),
∵A(4,0),C(0,2),
∴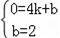
 ,解得
,解得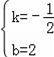
 ,
,
∴直线AC的解析式为y=﹣
 x+2.
x+2.
设直线BD的解析式为y=ax+c(a≠0),
∵B(0,3),D(1,0),
∴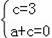
 ,解得
,解得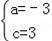
 ,
,
∴直线BD的解析式为y=﹣3x+3,
∴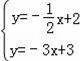
 ,解得
,解得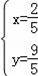
 ,
,
∴G(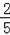
 ,
,
 ),
),
∴DG=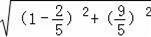
 =
=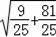
 =
=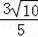
 .
.
过点D作DF⊥AC于点F,
∵直线AC的解析式为y=﹣
 x+2,
x+2,
∴设直线DF的解析式为y=2x+d,
∵D(1,0),
∴2+d=0,解得d=﹣2,
∴设直线DF的解析式为y=2x﹣2,
∴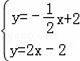
 ,解得
,解得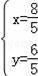
 ,
,
∴F(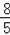
 ,
,
 ),
),
∴DF=
 =
=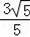
 ,
,
∴sin∠DGF=
 =
=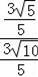
 =
=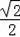
 ,
,
∴∠DGF=45°,即直线BD与AC所成的锐角是45°.


【点评】本题考查了二次函数综合题,涉及待定系数法求函数解析式、三角形面积公式、函数图象上点的坐标特征等知识,综合性强,值得关注.


 B.
B. C.
C. D.
D.

 x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
 的解集是 .
的解集是 .

 =3﹣x,则x的取值范围是 .
=3﹣x,则x的取值范围是 .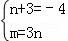 .解得:n=﹣7,m=﹣21 ∴另一个因式为(x﹣7),m的值为﹣21
.解得:n=﹣7,m=﹣21 ∴另一个因式为(x﹣7),m的值为﹣21