题目内容
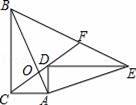
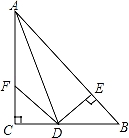
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为 .

14 .
【考点】旋转的性质.
【分析】根据旋转的性质可得AC=AD,AB=AE,∠CAD=∠BAE,再根据等腰三角形两底角相等求出∠ACD=∠ABE,从而得到△AOC∽△FOB,根据相似三角形对应边成比例求出BF=OB,过点C作CH⊥AB于H,根据等腰三角形三线合一的性质可得AO=2AH,再由△ACH∽△ABC求出AH,然后根据BO=AB﹣AO即可得解.
【解答】解:∵△ABC以点A为旋转中心顺时针旋转得到△ADE,
∴AC=AD,AB=AE,∠CAD=∠BAE(为旋转角),
∵∠ACD=
 (180°﹣∠CAD),∠ABE=
(180°﹣∠CAD),∠ABE=
 (180°﹣∠BAE),
(180°﹣∠BAE),
∴∠ACD=∠ABE,
又∵∠AOC=∠BOF,
∴△AOC∽△FOB,
∴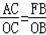
 ,
,
∵AC=OC,
∴BF=OB,
过点C作CH⊥AB于H,则AO=2AH,
∵△ACH∽△ABC,
∴AC2=AH•AB,
∴62=18•AH,
∴AH=2,
∴AO=4,
∴BF=BO=AB﹣AO=18﹣4=14.
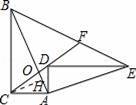

【点评】本题考查了旋转的性质,等腰三角形两底角相等的性质,等腰三角形三线合一的性质,利用三角形相似求出BF=OB是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.
B. C.
C. D.
D.

 x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=
x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=
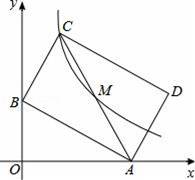


 的解集是 .
的解集是 .
 -
- =1无解,则
=1无解,则 =( )
=( )