题目内容
3．将一根长20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，设其中一段铁丝长为4x cm，两个正方形的面积和为y cm2（1）求y与x的函数关系式；
（2）要使这两个正方形面积之和为17cm2，那么这根铁丝剪成两段后的长度分别是多少？
（3）要使这两个正方形面积之和最小，则这根铁丝剪成两段后的长度各是多少？这两个正方形面积之和最小为多少？
分析 （1）由题意可知：设其中一段长为4xcm，则另一段长为20-4xcm，根据正方形面积和周长的转化关系“正方形的面积=$\frac{1}{16}$×周长×周长”列出面积的函数关系式；
（2）当y=17时，列方程即可得到结论；
（3）根据函数的性质求得最值．
解答 解：（1）设一段铁丝的长度为4x，另一段为（20-4x），则边长分别为x，$\frac{1}{4}$（20-4x）=5-x，
则y=x2+（5-x）（5-x）=2x2-10x+25；
（2）1当y=17时，
即2x2-10x+25=17，
解得：x=1，或x=4，
故这根铁丝剪成两段后的长度分别是4cm，16cm．
（3）∵y=2x2-10x+25=2（x-$\frac{5}{2}$）2+12.5，
∴剪成两段均为10cm的长度时面积之和最小，最小面积和为12.5cm2．
点评 本题考查了二次函数的最值，正方形的性质，列出关系式并整理成顶点式形式是解题的关键．
练习册系列答案
相关题目
14．两年前生产某药品的成本是5000元，现在生产这种药品的成本是3000元，设该药品成本的年平均下降率为x，则下面所列方程中正确的是（ ）
| A． | 5000（1-2x）=3000 | B． | 3000（1+2x）=5000 | C． | 3000（1+x）2=5000 | D． | 5000（1-x）2=3000 |
11．
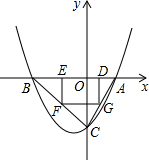如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：
（1）求抛物线表达式及A、B、C三点的坐标；
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并求出面积的最大值及m的取值范围．
如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：| x | … | -3 | -2 | 1 | 2 | … |
| y | … | $-\frac{5}{2}$ | -4 | $-\frac{5}{2}$ | 0 | … |
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并求出面积的最大值及m的取值范围．
口袋中有1个1元硬币和2个5角硬币，搅匀后从中摸出1个硬币，可能会出现的结果为1元硬币，5角硬币，5角硬币；将硬币放回再搅匀后摸出1个硬币，2次都是1元硬币的机会为$\frac{1}{9}$，都是5角硬币的机会为$\frac{2}{9}$．若用树形图表示如下，请填全．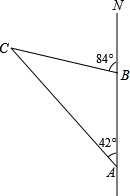
如图，一只船从A处出发，以18海里/时的速度向正北航行，经过10小时到达B处，分别从A、B处望灯塔C，测得∠MAC=42°，∠NBC=84°，则B与灯塔C的距离为180海里．
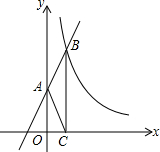如图，直线y=2x+2与y轴交于A点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点B，过点B作BC⊥x轴于点C，连接AC，若tan∠ACO=2，则此反比例函数解析式为y=$\frac{4}{x}$．