题目内容
12.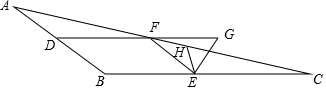 如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.
如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.
分析 先判定四边形BDFE是平行四边形,得出∠B=∠DFE,再设∠B=∠DFE=α,则∠FEC=α,根据△HEF中,∠HEC+∠EHC+∠C=180°,得到$\frac{1}{2}$(180°-α)+$\frac{1}{2}$α+40°+∠C=180°,再根据∠DFE-∠C=130°,得到α-∠C=130°,最后通过解方程组,可得α=144°.
解答 解:∵DF∥BC,EF∥AB,
∴四边形BDFE是平行四边形,
∴∠B=∠DFE,
设∠B=∠DFE=α,则∠FEC=α,
∵EG平分∠FEC,
∴∠GEC=$\frac{1}{2}$α,∠BEG=180°-α,
∵EH平分∠BEG,
∴∠HEG=$\frac{1}{2}$(180°-α),
∵△HEF中,∠HEC+∠EHC+∠C=180°,
∴$\frac{1}{2}$(180°-α)+$\frac{1}{2}$α+40°+∠C=180°,①
又∵∠DFE-∠C=130°,
∴α-∠C=130°,②
由①+②,可得α=144°,
∴∠B的度数为144°.
故答案为:144°.
点评 本题主要考查了平行四边形的性质,三角形内角和定理以及角平分线的定义的综合应用,解决问题的关键是根据角的和差关系,列出方程组进行求解.解题时注意方程思想的灵活运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7. 在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,则∠A的度数为( )
在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,则∠A的度数为( )
 在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,则∠A的度数为( )
在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,则∠A的度数为( )| A. | 80度 | B. | 50度 | C. | 100度 | D. | 110度 |
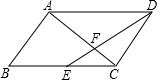 已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示) 计算:
计算: 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3). 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),图象与y轴交于点C(0,3),与x轴交于A、B两点.