题目内容
20.求证:等腰三角形两腰中线的交点在底边的垂直平分线上.分析 根据等腰三角形的性质得到∠ABC=∠ACB,AD=$\frac{1}{2}AB$,AE=$\frac{1}{2}AC$,得到AD=AE,推出△ABE≌△ACD,根据全等三角形的性质得到∠1=∠2,于是得到∠3=∠4,根据等腰三角形的判定得到OB=OC,即可得到结论.
解答  已知:在△ABC中,AB=AC,D,E分别是AB,AC的中点,CD,BE交于O,
已知:在△ABC中,AB=AC,D,E分别是AB,AC的中点,CD,BE交于O,
求证:点O在BC的垂直平分线上.
证明:∵AB=AC,D,E分别是AB,AC的中点,
∴∠ABC=∠ACB,AD=$\frac{1}{2}AB$,AE=$\frac{1}{2}AC$,
∴AD=AE,
在△ABE与△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠A=∠A}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD;
∴∠1=∠2,
∴∠ABC-∠1=∠ACB-∠2,
即∠3=∠4,
∴OB=OC,
∴点O在BC的垂直平分线上.
点评 本题考查了等腰三角形的性质,全等三角形的判定和性质,线段垂直平分线的判定,正确的作出图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
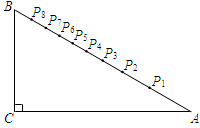 如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°. 如图,
如图, 如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,证明:△ABC∽△CDE.
如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,证明:△ABC∽△CDE.