题目内容
19.使分式$\frac{{{x^2}+1}}{1-3x}$的值为负的条件是( )| A. | x<0 | B. | x>0 | C. | x>$\frac{1}{3}$ | D. | x<$\frac{1}{3}$ |
分析 根据分式$\frac{{{x^2}+1}}{1-3x}$的值为负,以及x2+1>0,可得1-3x<0,据此求出x的取值范围即可.
解答 解:∵分式$\frac{{{x^2}+1}}{1-3x}$的值为负,x2+1>0,
∴1-3x<0,
解得x>$\frac{1}{3}$.
故选:C.
点评 此题主要考查了分式的值,以及一元一次不等式的求法,要熟练掌握.

练习册系列答案
相关题目
11.下列等式中是一元一次方程的是( )
| A. | S=$\frac{1}{2}$ab | B. | x-y=0 | C. | x=0 | D. | $\frac{1}{2x+3}$=1 |
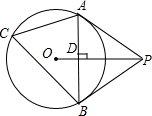 如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.
如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D. 如图,已知l1∥l2,∠A=40°,∠1=60°,求∠2的度数.
如图,已知l1∥l2,∠A=40°,∠1=60°,求∠2的度数. 一棵树(AB)和一根木杆(CD)在同一时刻的投影如图所示,木杆CD高3米,影子DE长2米;若树的影子BE长6米,则树AB长多少米?
一棵树(AB)和一根木杆(CD)在同一时刻的投影如图所示,木杆CD高3米,影子DE长2米;若树的影子BE长6米,则树AB长多少米? 如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.
如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.