题目内容
8．
如图，CD⊥AB，垂足为D，如果CD=12，AD=16，BD=9，那么△ABC是直角三角形吗？请说明理由．
分析 在Rt△ACD中利用勾股定理可求AC2，同理在Rt△ABD中利用勾股定理可求BC2，而AB=AD+BD，易求AC2+BC2=AB2，从而可知△ABC是直角三角形．
解答 解：是，理由如下：
∵CD⊥AB，CD=12，AD=16，BD=9，
∴AC2=CD2+AD2=400，
又∵CD⊥AB，AD=16，BD=9，
∴BC2=CD2+BD2=225，
∵AB=AD+BD=25，
∴AB2=625，
∴AC2+BC2=625=AB2，
∴△ABC是直角三角形．
点评 本题考查勾股定理、勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
相关题目
19．
如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AO=4，则AB的长是（ ）
如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AO=4，则AB的长是（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 8 |
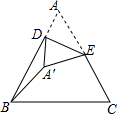如图，△ABC中，AB=BC=AC=10，D是AB边上的动点，E是AC边的中点，将△ADE沿DE翻折得到△A′DE，连接BA′，则BA′的最小值是5$\sqrt{3}$-5．
3．下列说法正确的是（ ）
| A． | 1-xy是单项式 | B． | ab没有系数 | ||
| C． | -5是一次一项式 | D． | -a2b+ab-abc2是四次三项式 |
如图所示，在菱形ABCD中，AB=2，∠BAD=60°，E是边AD的中点，M是边AB上任一点（不与点A重合），延长ME交CD的延长线于点N，连接MD、AN．