题目内容
11．
如图，双曲线y=$\frac{6}{x}$（x＞0）经过线段AB的中点M，则△AOB的面积为（ ）| A． | 18 | B． | 24 | C． | 6 | D． | 12 |
分析 设点M的坐标为（m，n），由点M为线段AB的中点即可得知点A（2m，0）、点B（0，2n），再根据反比例函数图象上点的坐标特征结合三角形的面积即可求出S△AOB的值．
解答 解：设点M的坐标为（m，n），则点A（2m，0），点B（0，2n），
∵点M在双曲线y=$\frac{6}{x}$（x＞0）上，
∴mn=6，
∴S△AOB=$\frac{1}{2}$OA•OB=2mn=12．
故选D．
点评 本题考查了反比例函数图象上点的坐标特征以及三角形的面积，设出点M的坐标，根据点M为线段AB的中点找出点A、B的坐标是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某生物兴趣小组在四天的实验研究中发现：骆驼的体温会随外部环境温度的变化而变化，而且在这四天中每昼夜的体温变化情况相同，他们将一头骆驼前两昼夜的体温变化情况绘制成右图，请根据图象回答：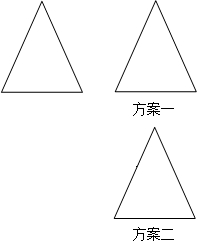
张倩同学打算制作一个平行四边形纸板，但手中只有一块等腰三角形纸板．张倩同学想了一下，用剪刀只剪了一刀，便得到一个平行四边形，且纸板充分利用没有浪费．你知道张倩是怎样剪的吗？用虚线表示出剪刀线；并请你画出两种张倩所拼的平行四边形．
19．
在平面直角坐标系中，若干个半径为2个单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，沿这条曲线向右上下起伏运动，点在直线上的速度为2个单位长度/秒，点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒，则2017秒时，点P的坐标是（ ）
在平面直角坐标系中，若干个半径为2个单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，沿这条曲线向右上下起伏运动，点在直线上的速度为2个单位长度/秒，点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒，则2017秒时，点P的坐标是（ ）| A． | （2017，0） | B． | （2017，$\sqrt{3}$） | C． | （2017，-$\sqrt{3}$） | D． | （2016，0） |
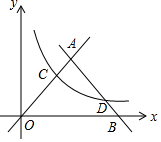在平面直角坐标系内，双曲线：y=$\frac{k}{x}$（x＞0）分别与直线OA：y=x和直线AB：y=-x+10，交于C，D两点，并且OC=3BD．
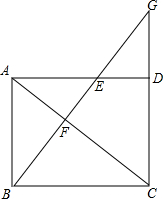已知：如图，在平行四边形ABCD中，AC为对角线，E是边AD上一点，BE⊥AC交AC于点F，BE、CD的延长线交于点G，且∠ABE=∠CAD．
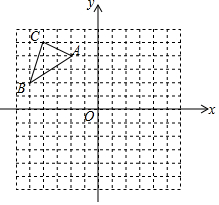已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位长度，再向下平移6个单位长度得到△A1B1C1．（图中每个小方格边长均为1个单位长度）．
1．下列图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |