题目内容
17. 已知:如图,∠ACB=∠ADB=90°,AC=AD,E是AB上任意一点.
已知:如图,∠ACB=∠ADB=90°,AC=AD,E是AB上任意一点.(1)BC与BD相等吗?试说明理由.
(2)CE=DE吗?为什么?
分析 (1)根据HL推出Rt△ACB≌Rt△ADB,根据全等三角形的性质推出即可;
(2)根据全等得出∠CAB=∠DAB,根据全等三角形的判定推出△ACE≌△ADE,根据全等三角形的性质得出即可.
解答 解:(1)BC=BD,
理由是:∵∠ACB=∠ADB=90°,
在Rt△ACB和Rt△ADB中
$\left\{\begin{array}{l}{AB=AB}\\{AC=AD}\end{array}\right.$AC=AD,AB=AB,
∴Rt△ACB≌Rt△ADB(HL),
∴BC=BD;
(2)CE=DE,
理由是:∵Rt△ACB≌Rt△ADB,
∴∠CAB=∠DAB,
在△ACE和△ADE中,
$\left\{\begin{array}{l}{AC=AD}\\{∠CAE=∠DAE}\\{AE=AE}\end{array}\right.$,
∴△ACE≌△ADE(SAS),
∴CE=DE.
点评 本题考查了全等三角形的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.已知抛物线C的解析式为y=ax2+bx+c,则下列说法中错误的是( )
| A. | a确定抛物线的形状与开口方向 | |
| B. | 若将抛物线C沿y轴平移,则a,b的值不变 | |
| C. | 若将抛物线C沿x轴平移,则a的值不变 | |
| D. | 若将抛物线C沿直线l:y=x+2平移,则a、b、c的值全变 |
2.七边形的外角和为( )
| A. | 1260° | B. | 900° | C. | 360° | D. | 180° |
9.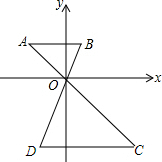 如图,已知△OAB与△OCD是相似比为1:3的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OCD内一点P′是一对对应点,则点P′的坐标是( )
如图,已知△OAB与△OCD是相似比为1:3的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OCD内一点P′是一对对应点,则点P′的坐标是( )
 如图,已知△OAB与△OCD是相似比为1:3的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OCD内一点P′是一对对应点,则点P′的坐标是( )
如图,已知△OAB与△OCD是相似比为1:3的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OCD内一点P′是一对对应点,则点P′的坐标是( )| A. | (-x,-y) | B. | (-3x,3y) | C. | (3x,-3y) | D. | (-3x,-3y) |
 将如图的直线补全成一条数轴,并在数轴上表示下列各数:2,-3,1.5,-$\frac{1}{2}$.再用“>”把它们连接起来.2>1.5>-$\frac{1}{2}$>-3.
将如图的直线补全成一条数轴,并在数轴上表示下列各数:2,-3,1.5,-$\frac{1}{2}$.再用“>”把它们连接起来.2>1.5>-$\frac{1}{2}$>-3.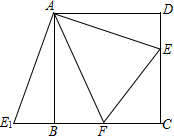 如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD的周长的一半.
如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD的周长的一半.
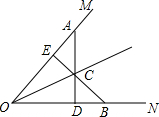 已知∠MON,用三角尺按下列方法画图:
已知∠MON,用三角尺按下列方法画图: