题目内容
5.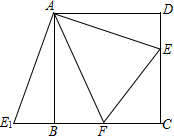 如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD的周长的一半.
如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD的周长的一半.
分析 根据旋转性质得出AE=AE1,BE1=DE,求出BE1+CF=DE+CF=CD,根据SAS推出△E1AF≌△EAF,根据全等三角形的性质得出EF=E1F,即可求出答案.
解答 证明:∵把△ADE顺时针旋转90°得△ABE1,
∴AE=AE1,BE1=DE,
∴BE1+CF=DE+CF=CD,
∵∠EAE1的平分线交BC边于点F,
∴∠E1AF=∠EAF,
在△E1AF和△EAF中
$\left\{\begin{array}{l}{A{E}_{1}=AE}\\{∠{E}_{1}AF=∠EAF}\\{AF=AF}\end{array}\right.$
∴△E1AF≌△EAF(SAS),
∴EF=E1F=BF+DE,
∴△CFE的周长=CE+CF+EF=CE+CF+BF+DE=CD+BC=正方形ABCD的周长的一半.
点评 本题考查了正方形的性质,全等三角形的性质和判定的应用,能求出△E1AF≌△EAF是解此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10.下列方程中没有实数根的是( )
| A. | x2-x-1=0 | B. | x2+3x+2=0 | C. | 2015x2+11x-20=0 | D. | x2+x+2=0 |
15.与4a2b2是同类项的是( )
| A. | 4ab | B. | -5a2b2 | C. | 3a3b | D. | -$\frac{1}{2}$ab3 |
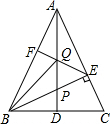 如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.
如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.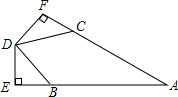 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F, 如图,已知AB=AC,点D在AC上,且AD=BD=BC,则∠ABD的度数为36°.
如图,已知AB=AC,点D在AC上,且AD=BD=BC,则∠ABD的度数为36°. 已知:如图,∠ACB=∠ADB=90°,AC=AD,E是AB上任意一点.
已知:如图,∠ACB=∠ADB=90°,AC=AD,E是AB上任意一点.