��Ŀ����
14�� ��֪������y=-$\frac{1}{2}$x2+bx+c��x���ڵ�A��B����y���ڵ�C���ı���OCDBΪ�����Σ���D������Ϊ��6��6����
��֪������y=-$\frac{1}{2}$x2+bx+c��x���ڵ�A��B����y���ڵ�C���ı���OCDBΪ�����Σ���D������Ϊ��6��6������1���������ߵĽ���ʽ��
��2����PΪ�߶�CD��һ���㣬��ÿ��2��λ���ٶ��ɵ�C���յ�D�˶�������OP��ȡOP���е�M��CD���������ڵ�E������EM�����P���˶�ʱ��Ϊt����PME�����ΪS����S��t�ĺ�����ϵʽ����ֱ��д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£�����MD��ֱ��y=mx-6������B����NΪֱ��y=mx-6��һ�㣬����DMN=90�㣬BN=2$\sqrt{2}$ʱ����x���Ϸ����������ϴ��ڵ�Q��ʹ��AOQ��������ڡ�PME����������ʱQ������꣮
���� ��1������õ�C��0��6����B��6��0����Ȼ��B��C��������������ߵĽ���ʽ�����b��c��ֵ��
��2����y=6���������ߵĽ���ʽ����õ�E�����꣬��0��t��4ʱ��PE=4-t����4��t��6ʱ��PE=6-t�����е����깫ʽ�ɵõ���M�����꣬������������ε������ʽ��⼴�ɣ�
��3������B���������y=mx-6�����m��ֵ���Ӷ��õ�ֱ��BN�Ľ���ʽΪy=x-6������������BN=2$\sqrt{2}$���ɵõ�N������Ϊ��8��2����4��-2������N������Ϊ��8��2��ʱ����MDN��90�㣬�������⣻����N������Ϊ��4��-2��ʱ�����ݹ��ɶ������涨���г�����t�ķ��̣��Ӷ������t��ֵ��Ȼ��ɵõ���PEM�������Ȼ�����������ε������ʽ�����Q�������꣬�����Q����������������ߵĽ���ʽ����õ�Q�ĺ����꣮
��� �⣺��1�����ı���OCDBΪ�����Σ���D������Ϊ��6��6����
��C��0��6����B��6��0����
����B��C��������������ߵĽ���ʽ�ɵõ�$\left\{\begin{array}{l}{-\frac{1}{2}��36+6b+c=0}\\{c=6}\end{array}\right.$����ã�$\left\{\begin{array}{l}{b=2}\\{c=6}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+2x+6��
��2����y=6���������ߵĽ���ʽ�ã�-$\frac{1}{2}$x2+2x+6=6�����x=0��x=4��
���E��������4��6����
��0��t��4ʱ����ͼ1��ʾ����PE=4-t��
��MΪOP���е㣬
��M��������$\frac{1}{2}$t��3����
���PEM�����=$\frac{1}{2}$��3����4-t��=-$\frac{3}{2}$t+6��
��4��t��6ʱ����ͼ2��ʾ��PE=6-t��
���PEM�����=$\frac{1}{2}$��3����t-4��=$\frac{3}{2}$t-6��
��S��t�ĺ�����ϵʽΪS=$\left\{\begin{array}{l}{-\frac{3}{2}t+6��0��t��4��}\\{\frac{3}{2}t-6��4��t��6��}\end{array}\right.$��
��3������B���������y=mx-6�ã�6m-6=0�����m=1��
��ֱ��BN�Ľ���ʽΪy=x-6��
�֡�BN=2$\sqrt{2}$��
���N��������8��2����4��-2����
����N������Ϊ��8��2��ʱ����MDN��90�㣬�������⣻
����N������Ϊ��4��-2��ʱ����ͼ3��ʾ��
�ߵ�M��$\frac{1}{2}$t��3����D��6��6����N��4��-2������DMN=90�㣬
��MD2+MN2=DN2������6-$\frac{1}{2}$t��2+��6-3��2+��4-$\frac{1}{2}$t��2+��-2-3��2=22+82��
�����ã�t2-20t+36=0����ã�t=2��t=18����ȥ����
��t=2ʱ��S=-$\frac{3}{2}$t+6=3������PEM�����Ϊ3��
��y=0���������ߵĽ���ʽ�ã�-$\frac{1}{2}$x2+2x+6=0����ã�x=-2��x=6��
���A��������-2��0����
��OA=2��
��$\frac{1}{2}$��AO��Qy=3����$\frac{1}{2}$��2��Qy=3����ã�Qy=3��
��y=3���������ߵĽ���ʽ�ã�-$\frac{1}{2}$x2+2x+6=3�������ã�x2-4x-6=0��
��ã�x=$\sqrt{10}$+2��x=-$\sqrt{10}$+2��
���Q��������$\sqrt{10}$+2��3����-$\sqrt{10}$+2��3����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ�����ɶ������涨���������ľ��빫ʽ�������ε������ʽ����õ�M�������ǽ���Ĺؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 4$\sqrt{3}$ | B�� | 8$\sqrt{3}$ | C�� | 10$\sqrt{3}$ | D�� | 12$\sqrt{3}$ |
 ��ͼ��ʾ������ͼ�εĸ���ͼ�ǣ�������
��ͼ��ʾ������ͼ�εĸ���ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | 0.2 | B�� | -5 | C�� | -$\frac{1}{5}$ | D�� | 5 |
| A�� | a=-3 | B�� | a=1 | C�� | a=3 | D�� | a=-1 |
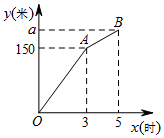 �ס����������̶�ͬʱ��ʼά��ijһ��·�棬һ��ʱ��ӱ��������ҶӶ��������ʣ���ά��������֪�Ҷ�ÿСʱά��·��ij��ȱ��ֲ��䣬��ÿСʱά��·��30�ף��ס��������ڴ�·��ά��·����ܳ���y���ף���ά��ʱ��x��ʱ��֮��ĺ���ͼ����ͼ��ʾ��
�ס����������̶�ͬʱ��ʼά��ijһ��·�棬һ��ʱ��ӱ��������ҶӶ��������ʣ���ά��������֪�Ҷ�ÿСʱά��·��ij��ȱ��ֲ��䣬��ÿСʱά��·��30�ף��ס��������ڴ�·��ά��·����ܳ���y���ף���ά��ʱ��x��ʱ��֮��ĺ���ͼ����ͼ��ʾ��