题目内容
5.菱形的周长为16,且有一个内角为60°,则此菱形的面积为( )| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 10$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
分析 作出草图,根据菱形的周长先求出边长AB,然后判断出△ABC是等边三角形,然后根据等边三角形的性质求出高,再利用菱形的面积公式计算即可得解.
解答 解:如图所示,
∵菱形的周长为16,
∴边长AB=BC=16÷4=4,
∵一个内角∠B=60°,
∴△ABC是等边三角形,
过点A作AE⊥BC于点E,
则BE=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2,
根据勾股定理,AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=2$\sqrt{3}$,
所以,菱形的面积为4×2=8$\sqrt{3}$,
故选:B.
点评 本题考查了菱形的性质,等边三角形的判定,能够正确画出图形和求出菱形边上的高是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知点(1,y1),(2,y2)是抛物线y=x2-6x上的两点,则y1,y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
16.下列几何体中,不属于棱柱的是( )
| A. |  | B. |  | C. |  | D. |  |
13.12×$\frac{5}{6}$的结果是( )
| A. | 10 | B. | 4 | C. | 6 | D. | 8 |
20.如果多边形的内角和是外角和的k 倍,那么这个多边形的边数是( )
| A. | k | B. | 2 k+l | C. | 2 k+2 | D. | 2 k-2 |
10.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
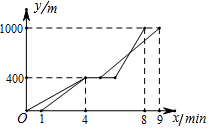 甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( )
甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( ) 已知抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于点A,B,交y轴于点C,四边形OCDB为正方形,点D的坐标为(6,6).
已知抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于点A,B,交y轴于点C,四边形OCDB为正方形,点D的坐标为(6,6).