题目内容
8. 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )| A. | $\frac{9}{2}$ | B. | $\frac{27}{4}$ | C. | $\frac{24}{5}$ | D. | 12 |
分析 所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B的横纵坐标的积即是反比例函数的比例系数.
解答 解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BD=3AD,
∴D($\frac{a}{4}$,b),
∵点D,E在反比例函数的图象上,
∴$\frac{ab}{4}$=k,∴E(a,$\frac{k}{a}$),
∵S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE=ab-$\frac{1}{2}$$•\frac{ab}{4}$-$\frac{1}{2}$k-$\frac{1}{2}$$•\frac{3a}{4}$•(b-$\frac{k}{a}$)=9,
∴k=$\frac{24}{5}$,
故选C.
点评 此题考查了反比例函数的综合知识,利用了:①过某个点,这个点的坐标应适合这个函数解析式;②所给的面积应整理为和反比例函数上的点的坐标有关的形式.

练习册系列答案
相关题目
13. 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )| A. | 2.4cm | B. | 4.8cm | C. | 5cm | D. | 9.6cm |
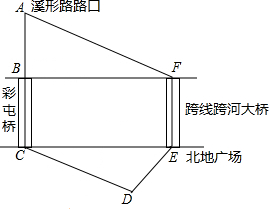 如图,家住彩屯溪形路路口的小李要经过彩屯到北地广场附近上班,路线为A→B→C→D→E.市政府决定修建设北地到彩屯的跨线跨河大桥EF,如果大桥建成后小李就可以由新大桥直线上班,路线A→F→E,BC∥EF,AB⊥BF,DE⊥CD,AB=420米,BC=300米,∠AFB=37°,∠CED=53°,请你帮助计算一下,小李改由新大桥上班会比原先少走多少米?(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,家住彩屯溪形路路口的小李要经过彩屯到北地广场附近上班,路线为A→B→C→D→E.市政府决定修建设北地到彩屯的跨线跨河大桥EF,如果大桥建成后小李就可以由新大桥直线上班,路线A→F→E,BC∥EF,AB⊥BF,DE⊥CD,AB=420米,BC=300米,∠AFB=37°,∠CED=53°,请你帮助计算一下,小李改由新大桥上班会比原先少走多少米?(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)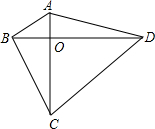 如图,四边形ABCD的对角线ACBD相交于点O,已知:OA=1,OB=2,OC=3,OD=4,CD=5.试求:
如图,四边形ABCD的对角线ACBD相交于点O,已知:OA=1,OB=2,OC=3,OD=4,CD=5.试求:
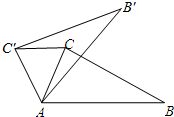 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB等于50°.
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB等于50°.